Să se determine m real dacă există o singură pereche (x,y) de numere reale
astfel încât: ![]()
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Aţi copiat greşit enunţul din imaginea ataşată.
Fie (x0,y0) acea pereche (unică) care verifică ambele inecuaţii. Dar atunci şi (y0,x0) verifică inecuaţiile, deci din unicitate, deducem x0=y0.
Rămâne ca inecuaţia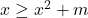 să fie verificată de un singur x real, ceea ce se întâmplă pentru m=1/4, pentru care singurul x este x=1/2.
să fie verificată de un singur x real, ceea ce se întâmplă pentru m=1/4, pentru care singurul x este x=1/2.
da, scuze. am corectat acum
multumesc!
Ecuatia nu este x^2>=x+m?? ,nu inteleg de unde ati obtinut-o.
am gresit eu enuntul. cel din imagine e corect
Din cele două inecuatii rezultă
1)
2)
1) În acest caz rezultă deci
2) În acest caz rezultă deci
Soluţia este greşită. Un sistem de ecuaţii nu este echivalent cu ecuaţia obţinută prin scăderea (sau adunarea) lor. De altfel, se vede uşor că pentru m=-3/4 există mai multe soluţii, una care sare în ochi fiind (x,y)=(0,0).
A se vedea interpretarea geometrică de aici: http://tube.geogebra.org/student/m1120843.
Zona violet reprezintă punctele ale căror coordonate sunt soluţii ale sistemului.
Modificaţi cu mouse-ul valoarea lui m pentru a vedea când zona respectivă se reduce la un punct.
Soluţia este greşită. Un sistem de ecuaţii nu este echivalent cu ecuaţia obţinută prin scăderea (sau adunarea) lor. De altfel, se vede uşor că pentru m=-3/4 există mai multe soluţii, una care sare în ochi fiind (x,y)=(0,0).
A se vedea interpretarea geometrică de aici: http://tube.geogebra.org/student/m1120843.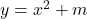 si respectiv
si respectiv 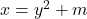 atunci cazurile 1) si 2) date de mine sunt solutii unice pentru fiecare dintre cele două valori ale lui
atunci cazurile 1) si 2) date de mine sunt solutii unice pentru fiecare dintre cele două valori ale lui  .Vă multumesc foarte mult pentru corectia făcută.
.Vă multumesc foarte mult pentru corectia făcută.
Zona violet reprezintă punctele ale căror coordonate sunt soluţii ale sistemului.
Modificaţi cu mouse-ul valoarea lui m pentru a vedea când zona respectivă se reduce la un punct.
Eu am spus că sunt două cazuri de studiat si greseala mea a fost că nu este permis să studiez separat cazurile de inegalităti stricte si de egalităti….
Frumoasă realizare cu programul GeoGebra pe care eu încerc de putin timp să-l învăt al utiliza…
Aveti dreptate!Cazul 2) gândit de mine nu verifică cerintele din problemă privind unicitatea solutiei.
––––––––––––––––
Dacă ar fi fost vorba în problemă doar de egalităti si anume de egalitătile
Din păcate, vă înşelaţi din nou. Sigur, dacă m=1/4, avem o unică pereche care satisface sistemul de ecuaţii (la acesta mă refer), aceeaşi ca în cazul sistemului de inecuaţii.
În schimb, dacă m=-3/4, sistemul de ecuaţii are două soluţii, anume (-1/2,-1/2) şi (3/2,3/2).
Din păcate, vă înşelaţi din nou. Sigur, dacă m=1/4, avem o unică pereche care satisface sistemul de ecuaţii (la acesta mă refer), aceeaşi ca în cazul sistemului de inecuaţii.
În schimb, dacă m=-3/4, sistemul de ecuaţii are două soluţii, anume (-1/2,-1/2) şi (3/2,3/2).
Aveti dreptate!Multumesc foarte mult si vă cer mii de scuze pentru tot deranjul care vi l-am făcut!Toată stima pentru ajutorul dat pentru mine ca de altfel si pentru toti ceilalti de pe acest forum in domeniul matematicii.