Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Am urmatorul exercitiu: intr-un grup de 6 persoane trebuie ales un presedinte, un vicepresedinte si o comisie formata din 2 persoane, din care nu pot face parte presedintele si vicepresedintele. In cate moduri diferite se poate face aceasta alegere?
Eu am calculat si am obtinut rezultatul 360, care a fost gresit, cel corect fiind 180. Imi poate explica cum s-a ajuns la acest rezultat?
Probabil că ai raţionat aşa: preşedintele se poate alege în 6 moduri, vicepreşedintele în 5, iar ultimele 2 persoane din acea comisie astfel-prima în 4 moduri, a doua în 3. Total 6*5*4*3=360.
Problema e la alegerea acelor ultime persoane. E totuna dacă primul ales e Stan, iar al doilea Bran, sau invers-primul e Bran şi al doilea Stan. Ordinea nu contează. Tu însă ai numărat ambele variante.
Corect e aşa: preşedintele se poate alege în 6 moduri, vicepreşedintele în 5, iar pentru comisia formată din 2 persoane dintre cele 4 rămase avem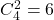
posibilităţi de alegere (alegem 2 persoane din patru, fără ca ordinea alegerii să conteze).
În total, obţinem 6*5*6=180 posibilităţi.
In cazul celor 2 persoane alese pentru comisie nu conteaza ordinea.
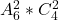
Pentru alegerea presedintelui si vicepresedintelui ordinea conteaza, pentru ca sunt roluri diferite. Asadar o posibila formula ar fi.
Multumesc, acum am inteles.😀