Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Buna. Am inceput relovarea problemei de mai jos si as dori
daca se poate sa ma ajutati sa o continui. Multumesc!
Enunt: Calculati sin3x+sin5x stiind ca x apartine (0, 45)
si cos4x=1.
Rezolvare: Am aplicat sina + sinb, deci
sin3x + sin5x = 2sin (3x+5x)/2 cos(3x-5x)/2=
=2sin (8x)/2 cos(-2x)2=
=2sin4x cos (-x)=
=2sin4x cosx
Dacă (0,45) înseamnă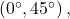
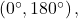
atunci unghiul 4x e în intervalul
iar în acest interval cosinusul nu ia valoarea 1.
In acest caz, cum pot continua rezolvarea?
sin3x=sin(4x-x)=sin4xcosx-sinx.cos4x ,Cum cos4x=1rezulta ca; (sin4x)^2=1-(cos4x)^2=0->sin4x=0deci sin3x=-sinx
sin5x=sin(4x+x)=sin4xcosx+sinx.cos4x=+sinx- deci sin3x+sin5x=-sinx+sinx=0
sin3x=sin(4x-x)=sin4xcosx-sinx.cos4x ,Cum cos4x=1rezulta ca; (sin4x)^2=1-(cos4x)^2=0->sin4x=0deci sin3x=-sinx
sin5x=sin(4x+x)=sin4xcosx+sinx.cos4x=+sinx- deci sin3x+sin5x=-sinx+sinx=0
Desigur, faptul că nu există nici un x care să verifice ipotezele problemei e un mic „detaliu” care nu trebuie să ne împiedice să o rezolvăm, nu?🙂
Noi rezolvam,nu gandim!