Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Se cere sa construim o primitiva a functiei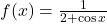 pe intervalul
pe intervalul ![Rendered by QuickLaTeX.com [0;\,2\pi]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-9d6a6c14bc28fefc4d78605a18fc1541_l3.png) pe care f este, evident, continua,
pe care f este, evident, continua,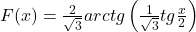 este o primitiva pe intervalele
este o primitiva pe intervalele ![Rendered by QuickLaTeX.com [0;\,\pi)\;si\;(\pi;\,2\pi].](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-53b1513e37b382c9a998ff23b04adfa9_l3.png)
![Rendered by QuickLaTeX.com F_1(x)=\begin{cases}F(x)+c_1\;\;pt.\;x\in [0;\,\pi)\\0\;\;\;pt.\;x=\pi\\F(x)+c_2\;pt.\;x\in (\pi;\,2\pi]\end{cases}.](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-1db78792502a1c531c9b41c8d36d9a84_l3.png)
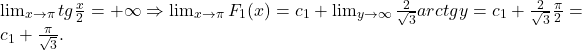
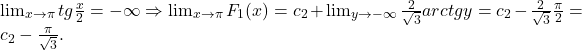
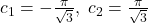 ne asiguram ca F_1 este continua in pi.
ne asiguram ca F_1 este continua in pi. 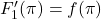 ?
?![Rendered by QuickLaTeX.com F'_1(x)=f(x)\;\forall x\in [0;\,\pi)\cup (\pi;\,2\pi];](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-017b67a66b0307e717b57fce8fbbc44e_l3.png)
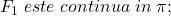
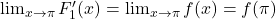 (pentru ca f este continua in pi)
(pentru ca f este continua in pi)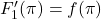 .
.
plecand de la faptul ca
O primitiva care sa ia valoarea 0 in pi poate sa arate astfel:
Sa determinam constantele a. i. functia propusa sa fie continua in pi, adica limitele laterale sa fie ambele 0.
La stanga,
La dreapta,
Deci luand
Dar ce ne asigura ca ea este derivabila in pi si, mai mult, ca
a)
b)
c)
sunt cele trei premise din Corolarul teoremei lui Lagrange, care, odata indeplinite, asigura ca
@ghioknt,la continuitate presupun ca ati schimbat variabila y=tg x/2,in fata lui tg x/2 mai era un radical nu l-ati „mancat” sau ati facut altceva cu el si nu observ eu?
Cat despre propozitia ” O primitiva care sa ia valoarea 0 in pi poate sa arate astfel” 0-ul a fost ales de dumneavostra cu un scop sau puteam alege orice alta constanta in pi si determinam c_1 si c_2 in functie de ce alegeam?
Rog sa fiti ingaduitor cu mine daca intrebarile sunt „banale” sau „non-sens” .sunt la inceput si vreau sa le „inteleg”
@ grapefruit
Noua variabila y include si factorul constant din fata lui tg(x/2).
Daca o functie admite o primitiva si aceasta se poate afla, atunci ea se afla abstractie facand de un termen contant (acel +C cu
care se incheie orice ..formula”). Asa ca exista o alegere a lui C astfel incat intr-un punct oarecare din I primitiva sa ia o anumita
valoare, nu neaparat 0. Aleg 0 din comoditate; daca as fi ales 2, ar fi trebuit sa scriu +2 de mai multe ori pe parcursul rezolvarii.