Pentru fiecare n ![]() N* consideram functia
N* consideram functia ![]() ,unde
,unde ![]() .
.
Aratati ca pentru n impar, functia ![]() are primitive daca si numai daca
are primitive daca si numai daca ![]()
Va multumesc !
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Se vede ca lim(n->infinit)(sin1/x)^n->0 si fn(x) este continua daca (lamda)n=0 si fn(x) are primitiva
(Motivarea primei afirmatii. Fie g(x)=x^2.cos(1/x). Avem g(x)continua in
x->0.Aplicand Lagange pe intervalul (0,x)avem;E= (g(x)-g(0))/x=2c.cos(1/c)+
sin(1/c), unde c apartine (0 , x) Pentru x->0 si c->0si exprsia E va fi E=0=0+sin(1/c) ,c->0. Deci lim(x->0)sin(1/x)->0)
Pai Lagrange se aplica pe un interval [a,b] cu a si b fixe , dar la toine [0, x) este variabil
Ignori informatia ca n = nr impar
1) Functia polinomiala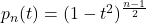 are o primitiva pe R, tot o functie polinomiala, P_n(t) (de grad n+1).
are o primitiva pe R, tot o functie polinomiala, P_n(t) (de grad n+1).![Rendered by QuickLaTeX.com Pt.\;x\neq 0:\;\left [ P_n(\cos \frac{1}{x}) \right ]'=p_n(\cos \frac{1}{x})\cdot \sin \frac{1}{x}\cdot \frac{1}{x^2}=\left [ 1-\cos^2 \frac{1}{x} \right ]^{\frac{n-1}{2}}\cdot \sin \frac{1}{x}\cdot \frac{1}{x^2}=f_n(x)\cdot \frac{1}{x^2}.](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-19f388c1c9df3626a5479ef2f0596a01_l3.png)
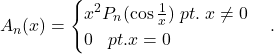
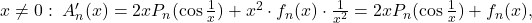 cf. obs. 2).
cf. obs. 2).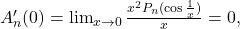 din motive lesne de inteles.
din motive lesne de inteles.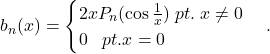
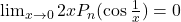 inseamna ca aceasta functie este continua pe R, inclusiv in 0,
inseamna ca aceasta functie este continua pe R, inclusiv in 0,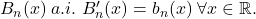
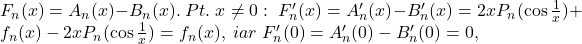 adica functia
adica functia 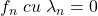 admite primitive.
admite primitive.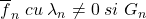 o primitiva a sa pe R.
o primitiva a sa pe R.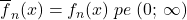 deducem ca, pe acest interval,
deducem ca, pe acest interval, 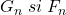 difera printru constanta, c.
difera printru constanta, c.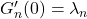 . (*)
. (*)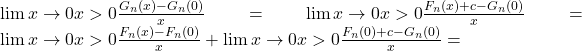
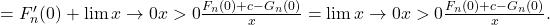
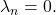
2)
3) Consider functia
Pt.
Pt. x=0:
4) Consider functia
Pentru ca
deci admite o primitiva pe R
5)Fie
6) Fie o functie
Pentru ca
Ar trebui sa avem
Dar
Ori, din doua una: ori numaratorul este 0 si atunci limita este 0, ori nu este 0 si atunci limita este infinita.
Deci relatia (*) nu poate avea loc decat pentru
@ghioknt,dar nu v-ati folosit ca n este impar,sigur autorul nu se gandea la o rezolvare asa grea si cu o imaginatie asa bogata(parerea mea).
Am folosit ca n este impar inca din prima propozitie cand am scris ca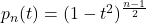 este o functie polinomiala.
este o functie polinomiala.
Pt. n par, exponentul nu ar fi natural, functia nu ar fi polinomiala, ci o functie putere (sau radical, cum doresti) si, mai grav pentru
mersul demonstratiei, nu ar avea primitive pe R, ci doar pe intervalul [-1; 1].
In primul rand problema este grea. Cat despre solutie, ea este destul de clasica, eu nu am facut decat sa numerotez
ideile principale, pentru ca cei ”pedepsiti” sa citeasca aceasta demonstratie sa poata reconstitui mai usor intregul din aceste
”prefabricate”. Cine gaseste undeva o solutie mai simpla este rugat sa o aduca la cunostinta, presupun ca nu numai eu, ci
si altii am fi interesati de asa ceva.