1.Multimea valorilor parametrului real m pentru care ecuatia
x(x-1)(x-2)(x-3)=m are toate radacinile reale este:
raspunsul corect este [-1,9/16].la indicatii spune ca notam y=x(x-3)
2.Daca ecuatia 2x^3 +mx^2 +4x+4=0 admite o radacina dubla,atunci m apartine multimii:
raspunsul corect este [-8,-5]
3.Fie P(x) un polinom de gradul 7 cu coeficientul lui x^7 egal cu 1.Daca exista a apartine lui R pentru care P(x)-a se divide cu (x+1)^4 si P(x)+a se divide cu (x-1)^4 atunci:
coeficientul lui x^5 este:raspunsul corect este -21/5
a este:raspunsul corect este 16/5
4.Fie polinomul P apartine lui C[x], P=x^3 +px+q cu radacinile x1,x2,x3.Sa se determine polinomul cu radacinile x1 patrat,x2 patrat,x3 patrat.
raspunsul corect este x^3 +2px^2 +xp^2 -q^2
5.Se considera polinoamele cu coeficienti complecsi P(x)=a0+a1X+…+anx^n si Q(x)=b0+b1x+…+bmx^m.Stiind ca polinomul Q(x) se divide cu x-1,sa se determine suma coeficientilor polinomului P(Q(x))
raspunsul corect este a0
La
: http://forum.matematic.ro/viewtopic.php?t=31325
La
:
Mai intai, din Relatiile lui Viète avem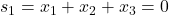
, 
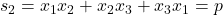si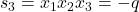 
.
Formam acum Sumele Viète corespunzatoare pentru a obtine polinomul.
Avem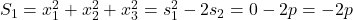
,
,
.
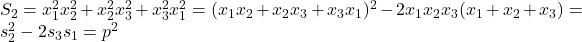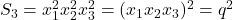Atunci polinomul cautat este,din Relatiile lui Viète,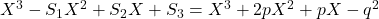
(doar ca o precizare: in cerinta apare 
de doua ori).
2). Fiind vorba despre o ecuatie algebrica, radacinile ei vor fi radacinile unui polinom, anume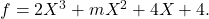
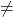0).
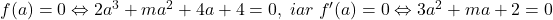(dupa simplificarea cu 2).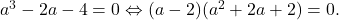
Polinomul f admite radacina dubla a daca si numai daca f(a)=0 si f'(a)=0 (iar f”(a)
Scadem prima relatie din cea de a doua inmultita cu a:
Evident, numai radacina reala a=2 poate fi radacina dubla; inlocuind in oricare dintre cele 2 relatii afli m=-7.
Asadar la intrebarea: carei multimi ii apartine m? raspunsul este: la orice multime care il contine pe -7.
Cinstit din partea ta este sa scrii toate raspunsurile la alegere, nu numai pe cel considerat corect,
La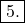
din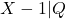 
rezulta 
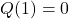. Acum stim ca suma coeficientilor unui polinom este data de valoarea acestuia in 
, deci suma coeficientilor lui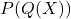 
este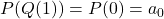 
, ceea ce trebuia aratat.
La 1)Fie functia; f(x)=x(x-1)(x-2)(x-3)=x^4-6x^3+11x^2-6x si s-o studiem. f ‘(x)=4x^3-18x^2+22x-6 Ec.f ‘(x)=0->x’1=(3-â5)/2 , x’2=3/2 ,
x’3=(3+â5)/2 de unde f((3-â5)/2)=-1 ; f(3+â5)/2)=-1 ; f(3/2)=9/16
………………………..Tabel de smne………………..
x…..l-inf,……………0…..(3-â5)/2…..1……3/2………2……..(3+â5)/2…..+inf.
f'(x).l- – – – – – – – – – – – – 0+ + + + + + 0- – – – – – – – – – 0+ + + + + +
f(x)..l scade…………………-1….creste……9/16….scade……..-1…creste……
Pentru a avea toate radacinle reale. ec f(x)=m ,trebue ca ”m ” apartine
[-1 , 9/16]
Domnule Phantomr,puteti detalia cum ati dedus ca suma coeficientilor lui P(Q(x)) este P(Q(1)) .Faza cu suma coeficientilor unui polinom P(x) este P(1)am inteles-o ,dar nu imi dau seama cum sa fac analogia cu P(Q(x)).
Late: Ce ziceti ,merge urmatorul rationament:
Dupa un numar finit de operatii putem aduce polinomul P(Q(x))=r_0+r_1x+…+r_nx^n,unde r_i reprezinta o combinatie intre coeficientii lui P(x) si Q(x). Acum daca notam P(Q(x))=R(x).Facand x=1,in amblele egalitati P(Q(1))=R(1),dar R(1) reprezinta suma coeficintetilor lui R(X) adica a lui P(Q(x),cum R(1)=P(Q(1)) deducem ca si P(Q(1)) semnifica acelasi lucru!
Este cam acelasi principiu..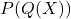
pe care sa-l notam, sa zicem, cu 
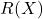este tot un polinom in 
, deci are forma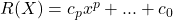 
si suma coeficietilor lui va fi 
.
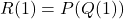EDIT: Da, ceva de genul🙂 .
@ghioknt,la problema 2 raspunsul nu este oarecum ciudat;daca raspunsul este acel interval s-ar subintelege ca orice m din intervalul ala verifica problema,dar trb interpretata ca exista cel putin un m din intervalul ala care sa verifice problema (am impresia).
Exista un singur interval la raspunsuri care-l contine pe -7
multumesc mult pentru raspunsuri!