Home/ Intrebari/Q 86819
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

marianstefi20
Pe: 2014-05-27T16:39:33+03:00 In: In:

Doua probleme admitere UTC Cluj

Buna seara tuturor!

De cateva ore bune ma chinui cu doua probleme pentru admitere.

Prima problema:

x,y,z sunt trei numere reale ce verifica relatia:
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z} = \frac{1}{x+y+z}$
Atunci:
$\frac{1}{x^{2n+1}}+\frac{1}{y^{2n+1}}+\frac{1}{z^{2n+1}} = ?$

$A. \quad \frac{(x+y+z)^n}{x^{2n+1}+y^{2n+1}+z^{2n+1}} \\ B. \quad \frac{1}{x^{2n+1}+y^{2n+1}+z^{2n+1}} \\ C. \quad \frac{n+1}{(x+y+z)^{2n+1}} \\ D. \quad \frac{n+1}{x^{2n+1}+y^{2n+1}+z^{2n+1}} \\ E. \quad \frac{2n+1}{(x+y+z)^{2n+1}}$

Raspunsul corect este B. Se si poate verifica gasind niste valori care sa satisfaca relatia, doar ca mi-as dori o metoda mai putin empirica, cel putin acum((-:. Aici ma sfatuise domnul PhatomR sa asociez egalitatii un polinom de gradul 3, ele fiind radacinile, dar nu am putut sa continui ideea sa.

A doua problema:
Fie m.n in $\mathbb{R}$ si $x_1,x_2,x_3$ radacinile ecuatiei: $x^3+mx+n = 0$ si matricea
A=

    $ \[ \left( \begin{array}{ccc} 1 & 1 & 1 \\ x_{_1} & x_{_2} & x_{_3} \\ x_{_1}^2 & x_{_2}^2 & x_{_3}^2 \end{array} \right)\] $

Determinantul matricei $A^2$ este ?
$ A. \quad -4m^3-27n^2 \\ B. \quad 4m^3-27n^2 \\ C. \quad -4m^3+27n^2 \\ D. \quad -2n^3-27n^2 \\ E. \quad -3n^3-27m^2 $
Raspunsul corect este A. Am incercat cu Viete, dar din nou se pare ca nu pot duce la capat vreun calcul.

Similare

10 raspunsuri

  1. PhantomR
    expert (VI)

    Cucubau!! 😀

    \fbox{1.}
    \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{x+y+z} \Leftrightarrow (x+y+z)(xy+yz+zx)=xyz. Notam s=x+y+z,p=xy+yz+zx,q=xyz. Atunci q=sp.

    Cu Relatiile lui Viète, x,y,z sunt radacinile ecuatiei:
    x^3-sx^2+px-q=0, deci x^3-sx^2+px-sp=0 \Leftrightarrow x^2(x-s)+p(x-s)=0 \Leftrightarrow (x-s)(x^2+p)=0. Deducem ca unul dintre numere este egal cu s. Sa zicem ca x. Atunci x=s=x+y+z \Rightarrow y+z=0 \Rightarrow z=-y, deci z,y au semne opuse, de unde deducem varianta corecta.

  2. grapefruit
    maestru (V)

    Cateva calcule la problema 2 poate te ajuta
    http://postimg.org/image/t23kx0667/

  4. marianstefi20

    Multumesc mult pentru prima problema PhantomR. Foarte frumoasa rezolvare. Chiar nu m-am prins…in plus nici nu aveam cum caci uitasem cu desavarsire de formarea ecuatiei polinomiale cu ajutorul sumelor Viete. Cat despre a doua problema am ajuns si eu la forma pe care domnul grapefruit a scris-o. Ce se dovedeste problematic pentru mine este sa reusesc cumva sa introduc relatiile Viete pe acolo.

  5. grapefruit
    maestru (V)

    Domnule PhantomR,puteti detalia cum se deduce varianta corecta,si o a doua intrebare daca luam cazul in care x^2+p=0 ce se intampla?

  6. PhantomR
    expert (VI)

    grapefruit wrote: Domnule PhantomR,puteti detalia cum se deduce varianta corecta,si o a doua intrebare daca luam cazul in care x^2+p=0 ce se intampla?

    Din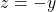 z=-y rezulta ca suma ceruta este egala cu \frac{1}{x^{2n+1}}.

    Tot folosind aceasta avem:

    A. \frac{x^n}{x^{2n+1}}=\frac{1}{x^{n+1}}
    B. \frac{1}{x^{2n+1}}
    C. \frac{n+1}{x^{2n+1}}
    D. \frac{n+1}{x^{2n+1}}<br/> E. [tex]\frac{2n+1}{x^{2n+1}}

    Deci B. e buna. Acum, A conduce la 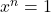x^n=1 pe care o putem eleminia caci aceasta relatie ar trebui sa aiba loc pentru orice n natural si orice x complex (caci orice triplet (x,a,-a) verifica relatia data). Dar pentru n=1 deducem x=1, deci nu se pastreaza generalitatea. Mai precis, avem , de exemplu, urmatorul contraexemplu: n=1,x=2,y=1,z=-1.

    C. implica 1=n+1 \Rightarrow n=0, contrazicand faptul ca relatia trebuie sa aiba loc pentru orice n natural.

    D. la fel ca l C
    E. rezulta 2n+1=1 \Rightarrow n=0, fals din motivele precizate la C.

    Acela nu e chiar un caz.. o radacina verifica x-s=0, iar celelalte x^2+p=0. Daca intrebarea se refera la ce informatii ajutatoare putem culege din x^2+p=0, un posibil raspuns ar fi aceeasi informatie ca la celalalt, caci ecuatia x^2=-p are solutii opuse: daca a este o radacina patrata a lui p, putem rescrie ecuatia ca (x+ip)(x-ip)=0, de unde solutiile sunt ip,-ip, de semne contrare (in cazul p=0, radacinile sunt ambele 0 si se verifica 0=-0).

  8. PhantomR
    expert (VI)

    marianstefi20 wrote: Multumesc mult pentru prima problema PhantomR. Foarte frumoasa rezolvare. Chiar nu m-am prins…in plus nici nu aveam cum caci uitasem cu desavarsire de formarea ecuatiei polinomiale cu ajutorul sumelor Viete. Cat despre a doua problema am ajuns si eu la forma pe care domnul grapefruit a scris-o. Ce se dovedeste problematic pentru mine este sa reusesc cumva sa introduc relatiile Viete pe acolo.

    Cu multa placere! ^_^ A doua e ciudata.. am sa ma mai gandesc la ea.

  9. grapefruit
    maestru (V)

    Multumesc,foarte bine explicat!

  10. PhantomR
    expert (VI)

    Cu multa placere! ^_^ Va multumesc si eu pentru apreciere!

  12. PhantomR
    expert (VI)

    \fbox{2.} Cred ca am gasit o solutie. Folosim faptul ca \det A^t = \det A.
    Avem atunci \det A^2=\det A\cdot \det A=\det A\cdot \det A^t=\det (A\cdot A^t).

    Calculand, avem A\cdot A^t = \left( \begin{matrix} 3 & x_1+x_2+x_3 & x_1^2+x_2^2+x_3^2 \\ x_1+x_2+x_3 & x_1^2+x_2^2+x_3^2 & x_1^3+x_2^3+x_3^3 \\ x_1^2+x_2^2+x_3^2 & x_1^3+x_2^3+x_3^3 & x_1^4+x_2^4+x_3^4 \end{matrix}\right).

    Vom calcula fiecare element al matricei anterioare folosind Relatiile lui Viète. Notand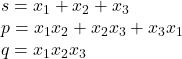 s=x_1+x_2+x_3 \\ p=x_1x_2+x_2x_3+x_3x_1 \\ q=x_1x_2x_3 avem s=0, p=m si q=-n.

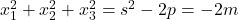    Avem x_1+x_2+x_3=s=0, apoi x_1^2+x_2^2+x_3^2=s^2-2p=-2m. Sa observam acum ca din x_1^3+mx_1+n=0 si analoagele, prin adunare rezulta \sum_{k=1}^3 x_k^3+m\sum_{k=1}^3 x_k+3n = 0 \Rightarrow \sum_{k=1}^3 x_1^3=-3n, deci x_1^3+x_2^3+x_3^3=-3n. Pentru ultima suma, avem x_1^3+mx_1+n=0 |\cdot x_1 \Rightarrow x_1^4+mx_1^2+nx_1=0 si analoagele, de unde prin adunare \sum_{k=1}^3x_k^4+m\sum_{k=1}^3 x_k^2+n\sum_{k=1}^3x_k=0 \Rightarrow \sum_{k=1}^3x_k^4+m(-2m)+0=0 \Rightarrow \sum_{k=1}^3x_k^4=2m^2, adica x_1^4+x_2^4+x_3^4=2m^2.

    Avem deci A\cdot A^t=\left( \begin{matrix} 3 & 0 & -2m \\ 0 & -2m & -3n \\ -2m & -3n & 2m^2\end{matrix}\right) si deci \det A^2 = \det (A\cdot A^t) = \left | \begin{array} 3 & 0 & -2m \\ 0 & -2m & -3n \\ -2m & -3n & 2m^2\end{array} \right | =-12m^3+0+0-(-8m^3+27n^2+0)=-12m^2+8m^2-27n^2=-4m^3-27n^2 si am obtinut exact raspunsul \fbox{A.}.

    NOTA: Dezvoltarea determinantului am facut-o cu Regula triunghiului. Se mai putea face un 0 daca se inmultea prima linie cu m si se aduna la ultima, dar nu ar fi fost oricum pe aceeasi linie/coloana cu celelalte doua. Alte zerouri ar fi mai greu de facut si cred ca e oarecum mai rapid asa (cel putin dupa mine).

  13. marianstefi20

    Mi se pare rezolvarea problemei de-a dreptul geniala. Chiar foarte interesanta ideea! Nu mi-ar fi venit deloc in minte sa fac asa ceva. Multumesc mult domnule PhatomR – ca de obicei…ideile sunt grozave.

Raspunde

Raspunde