Home/ Intrebari/Q 86197
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

flaviu_1
Pe: 2014-04-07T11:59:35+03:00 In: In:

sir

Fie (a_n)n>=0 un sir descrescator spre zero.
Limita sirului x_n=\sum_{k=0}^n(-1)^ka_{n+k} este:

A.0
B.1
C.+\infty
D.nu exista

Similare

4 raspunsuri

  1. DD
    profesor

    Fie sirul Yn=Suma(k de la 1 la n) [ l (-1)^k.a(n+k) l ] si termenul urmator acstui sir; Y(n+1)=Suma(k de la 1 la (n+1) l l (-1)^k.a(n+1+k) l ] . Cum ;
    a(n+k)>a(n+1+k) exista o valoare a lui n pentru care Yn>Y(n+1) si cum orice Yn>0 ,lim(n->infinit)Yn->0 si cu atat mai mult lim(x->infinit)Xn->0

  2. ella22

    De ce pentru sirul Yn pornim cu k de la 1 si nu de la 0?

  4. DD
    profesor

    Ai dreptate , din obisnuinta am pus 1. Scuze!

  5. ghioknt
    profesor

    Teorema lui Leibniz:Daca (a_n)_{n\geq 1} este un sir descrescator, convergent la 0, atunci sirul
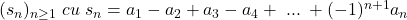    (s_n)_{n\geq 1}\;cu\;s_n=a_1-a_2+a_3-a_4+\;...\;+(-1)^{n+1}a_n este convergent.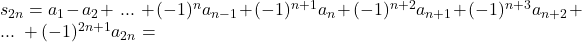
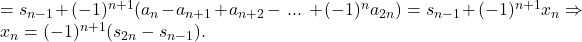
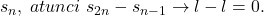
    Avem s_{2n}=a_1-a_2+\;...\;+(-1)^na_{n-1}+(-1)^{n+1}a_n+(-1)^{n+2}a_{n+1}+(-1)^{n+3}a_{n+2}+\;...\;+(-1)^{2n+1}a_{2n}=
    =s_{n-1}+(-1)^{n+1}(a_n-a_{n+1}+a_{n+2}-\;...\;+(-1)^na_{2n})=s_{n-1}+(-1)^{n+1}x_n\Rightarrow x_n=(-1)^{n+1}(s_{2n}-s_{n-1}).
    Daca notam cu l limita lui s_n,\;atunci\;s_{2n}-s_{n-1}\to l-l=0.
    Deci x_n se prezinta ca produsul dintre un sir marginit si unul convergent la 0; deci si x_n are limita 0.
    Teorema (criteriul) lui Leibniz nu este prea greu de demonstrat.
    Cu bine,
    ghioknt

Raspunde

Raspunde