Fie ![]() n>=1 si
n>=1 si ![]() n>=1 doua siruri de numere reale,
n>=1 doua siruri de numere reale,
![]() ,
,
![]() .
.
Daca ![]() ,atunci
,atunci
![]() =?
=?
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sirul ; bn=1+1/2+1/3+…..1/n-lnn este un sir descrescator ,
b(n+1)-bn=1/(n+1)-(ln(n+1)-lnn) Sa reamintim ca , daca f(x)=lnx conf.teoreme lui Lagrange pe intervalul(n , n+1) avem ln(n+1)-lnn=1/c ,unde n<c<n+1 sau
1/n>1/c>1/(n+1) de unde ;1/(n+1)-(ln(n+1)-lnn)<0. Deci b(n+1)-bn este un
sir descrescator si lumita lui nu este zero.Fie acum sirul .an=1+1/2+1/3+….1/n-ln(n+1). Sa facem si aici operatia ; a(n+1)-an=1/(n+1)-
(ln(n+2)-ln(n+1))> Luand din nou f(x)=lnx dr pe intervalul ((n+1) , (n+2))vom
avea ;ln(n+2)-ln(n+1)=1/c , unde n+1<c<n+2 sau 1/(n+2)<1/c<1/(n+1) sau ; 1/(n+1)-(ln(n+2)-ln(n+1))>0 < DE unde a(n+1).>an deci sirul este crescator In afara de acestea se vede usor ca an<bn, de unde cele doua siruri tind spre aceeasi limita .Lmita celor doua siruri s-a numit ”constanta lui Euler” , s-a notat cu „c” si s-a calculat ca c=0,5772….
Fie sirl; Cn=1+1/3+1/5+….+1/(2n-1)-(lnn)/2 unde (ln√n=(lnn)/2). Sa facem urmatoarea cosmetizare . Sa luam sirul dn=1/2+1/4+1/6….+1/(2n)-(lnn)/2 si cn+dn= [1+1/2+1/3+1/4+….+1/(2n)-lnn-ln2]+ln2=”c”+ln2.Dar dn=(1/2)*[1+1/2+1/3…+1/n-lnn)=”c”/2 Astfel in final , la limita,avem; lim(cn)+”c”/2= „c”+ln2 sau ; lim(cn)=c”/2+ln2.Cum in problema „c” s-a notat cu b si lim(cn) =c, rezulta ca; c=b/2+ln2
„an<bn, de unde cele doua siruri tind spre aceeasi limita”->Aceasta se intampla pe caz general?
Se vede ca an-bn=ln(n/(n+1))<0->an<bn si cand n->infinit an-bn->0
Domnule DD,nu inteleg o chestie ;sirul c_n+d_n nu formeaza tocmai sirul b_n;observ ca dumneavoastra ati scazut un ln2 si ati adunat un ln 2 si nu inteleg de ce sirul acela -ln2 tinde la c ;ca sa puteti afirma ca c_n+d_n=c+ln2
Cand sirul este 1+1/2+1/3+…1/(2n)rebue sa urmeze(-ln(2n)) Cum Cn+dn=1+1/2+1/3+….1/(2n)-lnn a trebuit sa adun si sa scad ln2 ,astfel -lnn-ln2=-ln(2n) dabia acum 1+1/2+1/3+….1/(2n)-ln(2n)=”c” asa ca :cn+dn=”c”+ln2 CLAR?
Marea problema este acea suma.
Avem . Observam asemanarea dintre sirurile
. Observam asemanarea dintre sirurile  , ceea ce conduce la considerarea subsirului
, ceea ce conduce la considerarea subsirului 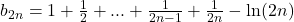 , deci
, deci  (1)
(1)
Acum, pentru a ajunge la acea suma din sirul , trebuie sa „scapam” de fractiile cu numitorul par, deci de suma
, trebuie sa „scapam” de fractiile cu numitorul par, deci de suma  (2).
(2).
Scazand (1),(2) avem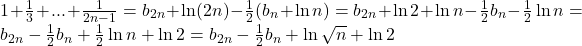 .
.
Acum, . Prin trecere la limita, deducem
. Prin trecere la limita, deducem  .
.
In concluzie, .
.
NOTA: Poate parea cam complicat, dar nu e chiar asa.. e putin cam lung deoarece am incercat sa explic cum se pot stabili relatiile dintre cele doua siruri.
In cazul in care avem sirul
 n>=1, sir de numere reale, astfel ca sirul
n>=1, sir de numere reale, astfel ca sirul
 ,n>=1, sa fie marginit, cum se poate afla limita sirului
,n>=1, sa fie marginit, cum se poate afla limita sirului  n>=1?
n>=1?
Se presupune cumva ca limita acestui exista (si e finita?)?
exista (si e finita?)?
Se specifica doar atat, iar variantele de raspuns sunt:





Va multumesc pentru informatii!
Consideram si
si  .
.
Sa aratam ca este marginit. Voi prezenta o demonstratie cu o idee similara cu cea pe care a prezentat-o domnul DD. Va multumesc pentru postare, domnule DD! ^_^
este marginit. Voi prezenta o demonstratie cu o idee similara cu cea pe care a prezentat-o domnul DD. Va multumesc pentru postare, domnule DD! ^_^
In acest sens, pentru orice , consideram functia
, consideram functia ![Rendered by QuickLaTeX.com f:[k,k+1]\to\mathbb{R},f(x)=\ln x](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-b613f4cf89ec6ca6056cb38c744b1911_l3.png) . Din Teorema lui Lagrange, exista
. Din Teorema lui Lagrange, exista ![Rendered by QuickLaTeX.com c\in [k,k+1]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-fc471e72732f95298f3bd0601ee71305_l3.png) cu
cu  . Cum
. Cum  . Noi vom avea nevoie doar de prima inegalitate, din care obtinem
. Noi vom avea nevoie doar de prima inegalitate, din care obtinem  . Adunam aceste inegalitati pentru
. Adunam aceste inegalitati pentru  si obtinem pentru
si obtinem pentru  ca
ca  , deci
, deci  , adica
, adica  e marginit.
e marginit.
NOTA: Acesta este un rezultat cunoscut, pe care v-ar putea ajuta si pe viitor sa il tineti minte.
Vom folosi acum urmatoarea proprietate pe care o voi demonstra in caz general: Daca sunt siruri marginite, atunci si sirul
sunt siruri marginite, atunci si sirul  este marginit. Intr-adevar, exista
este marginit. Intr-adevar, exista  cu
cu  si
si  . De aici si folosind Inegalitatea modulului, avem
. De aici si folosind Inegalitatea modulului, avem  , deci si
, deci si  e marginit.
e marginit.
Acum, cum noi stim ca e marginit si cum am aratat ca si
e marginit si cum am aratat ca si  are aceasta caracteristica, rezulta ca
are aceasta caracteristica, rezulta ca  e marginit, adica exista
e marginit, adica exista 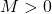 cu
cu  , adica
, adica  . Pentru
. Pentru  avem
avem  , deci rezulta
, deci rezulta  . Cum
. Cum  , din , deducem ca
, din , deducem ca  este un sir convergent, iar
este un sir convergent, iar  .
.
Foarte interesanta rezolvarea!Multumesc pentru explicatii…
Superb!
Cu multa placere!:) Va multumesc si eu pentru apreciere!
Multumesc! ^_^
Totusi ,revin si eu cu o curiozitate; daca a<x_n<b spunem ca sirul este marginit(am incadrat toate numerele sirului in alte 2 numere reale);o alta definitie a marginirii este |x_n|<M ;M>0 sau -M<x_n<M.(care dupa parerea mea nu sunt echivalente pt ca a doua definite este un caz particular a primei pt a=-b).
Sau teorema de fata precizeaza doar faptul ca sirul este marginit neoferind neaparat minorantul sau majorantul?
Spunem ca un sir este marginit daca exista doua numere reale
este marginit daca exista doua numere reale  astfel incat
astfel incat  .
.
Echivalent, un sir este marginit daca si numai daca exista un numar
este marginit daca si numai daca exista un numar 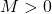 astfel incat
astfel incat  .
. Presupunem ca exista un astfel de
Presupunem ca exista un astfel de  . Din
. Din  , adica sirul este marginit.
, adica sirul este marginit.
 Presupunem ca sirul este marginit. Atunci exista numerele reale
Presupunem ca sirul este marginit. Atunci exista numerele reale  cu
cu  . Fie
. Fie  . Rezulta
. Rezulta  . In plus, avem
. In plus, avem 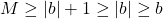 si
si  (ultima inegalitate provine din faptul ca
(ultima inegalitate provine din faptul ca 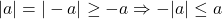 ). Din cele doua inegalitati, avem
). Din cele doua inegalitati, avem  , ceea ce inseamna ca
, ceea ce inseamna ca  .
.
Demonstratie:
NOTA: In alegerea lui in demonstratia implicatiei directe apar acei
in demonstratia implicatiei directe apar acei  pentru a ne asigura ca
pentru a ne asigura ca 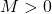 . Totusi, cazul in care
. Totusi, cazul in care  nu era asa greu de tratat separat, caci acesta e echivalent cu tex]|a|=|b|=0 \Rightarrow a=b=0 \Rightarrow x_n=0,\forall n\geq 1[/tex] si atunci orice numar
nu era asa greu de tratat separat, caci acesta e echivalent cu tex]|a|=|b|=0 \Rightarrow a=b=0 \Rightarrow x_n=0,\forall n\geq 1[/tex] si atunci orice numar 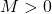 poate fi ales ca majorant, caci
poate fi ales ca majorant, caci  , pentru
, pentru 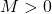 .
.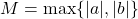 avem
avem 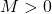 .
.
Deci, in ipoteza ca sirul nu are toti termenii nuli (caz in care am precizat o maniera de tratare mai sus), daca luam
Cu aceasta, rezultatul este demonstrat.
In legatura cu intrebarea despre majorant/minorant, nu sunt sigur daca inteleg bine. Dar as putea da urmatorul exemplu: daca noi stim ca , aceasta inseamna ca sirul e marginit. Ori, aceasta inseamna ca exista un
, aceasta inseamna ca sirul e marginit. Ori, aceasta inseamna ca exista un  cu
cu  . Teorema nu precizeaza exact expresia numerica a acestui
. Teorema nu precizeaza exact expresia numerica a acestui  , dar in cazul problemei precedente nu este nevoie de ea, ci este suficient sa stim ca acest numar finit exista.
, dar in cazul problemei precedente nu este nevoie de ea, ci este suficient sa stim ca acest numar finit exista.