Home/ Intrebari/Q 85066
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

dennis9091
guru (IV)
Pe: 2014-01-21T17:52:53+02:00 In: In:

tmmate 2012

Stiind ca x^2+y^2=1 atunci maximul expresiei |2x+3y| este …

Similare

6 raspunsuri

  1. ghioknt
    profesor

    Fie t o valoare a expresiei 2x+3y; Relaţia 2x+3y=t este ecuaţia unei drepte h, a cărei direcţie nu se schimbă dacă se
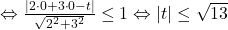
    modifică t (panta constanta, -2/3). Relaţia x^2+y^2=1 este ecuaţia unui cerc cu centrul în O(0, 0), cu r=1.
    O pereche (x, y) care verifică ambele relaţii reprezintă coordonatele unui punct aflat şi pe cerc şi pe dreapta h. O dreaptă h
    intersectează cercul <=> d(O;h)</=r\Leftrightarrow\frac{|2\cdot 0+3\cdot 0-t|}{\sqrt{2^2+3^2}}\leq 1\Leftrightarrow |t|\leq \sqrt{13}
    rezultat care spune că valoarea maximă a lui |t| este \sqrt{13}.
    Cu bine, ghioknt.

  2. Green eyes
    maestru (V)

    Salut,

    O altă variantă de rezolvare ar fi cu inegalitatea celebră a triumviratului 🙂 Cauchy-Buniakovski-Schwarz:

    (2x+3y)^{\small 2}\le(2^{\small 2}+3^{\small 2})\cdot(x^{\small 2}+y^{\small 2})=13\Rightarrow |2x+3y|\le\sqrt{13}

    Green eyes.

  4. ghioknt
    profesor

    Ai dreptate, cred că o asemenea soluţie aştepta dennis. Mie unuia nu mi-a plăcut soluţia mea, mi s-a părut un pic forţată
    pentru elevi de clasa a IX-a. Ar fi bine dacaă”beneficiarii” s-ar pronunţa în legătură cu soluţiile primite, puţini o fac.
    Apropo de triumvirat; termin de demonstrat inegalitatea şi mă trezesc întrebat: de ce se numeşte aşa, fiecare a descoperit
    câte o paranteză? 🙂
    Cu bine, ghioknt.

  5. dennis9091
    guru (IV)

    Va multumesc!

  6. Green eyes
    maestru (V)

    Bună seara domnule Ghioknt,

    Simpatică întrebarea aceea cu paranteza. Cred că în acea vreme, fiecare dintre cei 3 maeştri ai matematicii a descoperit individual celebra inegalitate, în ani diferiţi şi la capitole diferite ale matematicii.

    La acea vreme nu exista nici Internet, nici televiziune, exista cu siguranţă o efervescenţă creatoare (wow, am crezut că am uitat acest clişeu !). Nu toţi erau avuţi şi deci nu aveau uşor acces în înalta societate, aşa că încercau să se remarce prin talente de tot felul.

    Istoricii matematicii au decis se pare să dea celor 3 Cezari ceea ce li se cuvine, adică recunoaşterea oficială a descoperirii acestei inegalităţi fundamentale pentru matematica elementară şi nu numai.

    În ce domeniu activaţi ? La liceu, sau la facultate ? Cine au fost cei care v-au întrebat ?

    Cu respect,
    Green eyes.

  8. ghioknt
    profesor

    Bună seara Green eyes,
    În fiecare clasă există, se pare, un elev Bulă … Probabil că i-am captat atenţia din moment ce s-a arătat interesat de
    mecanismele descoperirilor în matematică. Mie nu mi-a rămas decât să-l apreciez: iată, ce-ai observat tu, este un exemplu
    de corespondenţă bijectivă între două mulţimi, să recunoaştem, destul de abstracte.
    O seară bună,
    ghioknt.

Raspunde

Raspunde