1. Se da ecuatia mx^2 +2(m+1)x + 8=0 si se cere:
b) sa se determine m astfel incat sa avem (x1^2+x2^2)/(x1x2) > x1+x2, x1 si x2 fiind radacinile ecuatiei date.
2.se dau ecuatiile x^2-(m+1)x+m2=0 cu radacinile x si x2 si y^2 -(m+3)y+12m +11=0 cu radacinile y1 si y2.
Sa se determine m astfel ca intre radacinile ecuatiei sa avem:
2(x1+x2)(y1+y2) mai mic sau egal decat x1x2+y1y2.
3. Se considera ecuatia de gradul al doilea: (1+a^2)x^2 – (1+a)x + a(1-a)=0.
Sa se determine parametrul a pentru care are loc inegalitatea:
-1<sau egal 1/x1+1/x2+1/x1x2 <sau egal 0.
Greeu si nu inteleg?
Salut,
Nu este deloc greu. Dacă te apuci de rezolvat şi nu ştii nimic despre ecuaţiile de gradul al II-lea (adică nu ştii teoria predată la şcoală), atunci normal că este greu.
Dacă ecuaţia este
şi rădăcinile ei sunt x1 şi x2, atunci: 
Apoi, trebuie să te foloseşti de:
Ţii cont de cele de mai sus, ajungi în fiecare caz la câte o inecuaţie, o rezolvi şi afli valorile lui m, sau pe a.
Exemplu, exerciţiul 3: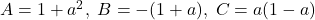
:
Inecuaţia de rezolvat este dublă: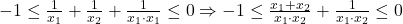
Înlocuieşti pe x1+x2 şi separat pe x1x2, separi inecuaţia dublă în 2 inecuaţii simple, le rezolvi, intersectezi soluţiile lor şi îl afli pe a.
Pentru rezolvarea inecuaţiilor trebuie să cunoşti semnul funcţiei de gradul al doilea, îţi recomand să re-citeşti teoria.
Spor la treabă !
Green eyes.