Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
lim (x–0) (rad(x^2+x+1)-1 )/(arcsin(x^3-x^2)) = lim (x+1)/((x^2-x)(rad(x^2+x+1)+1)) = acum daca trec la limita obtin 1/0 pot sa consider „prin omisiune” ca acel 0 este cu plus si limita sa aiba valoarea 00.
X^2=(1 -1
1 -1 ) nu are solutii, X matrice de ord in 2 M(C) .O solutie ar fi sa o rezolvam cu ajutorul sistemelor insa mi se pare prea laborioasa si incurcata metoda.As dori o alta abordare daca se poate.
În calculul limitelor scrierile ”+0” şi ”-0” sunt nişte ideograme pentru ”numitor pozitiv care tinde la 0”, respectiv, ”numitor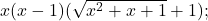
pot să iau o vecinătate a lui 0 suficient de mică (de ex. (-0,1; 0,1)) pe
, unde V este o vecinătate a lui a; analog pentru limita la dreapta.
negativ care tinde la 0”, sau, încă şi mai detaliat, pentru ”există o vecinătate a punctului în care calculăm limita pe care
numitorul ia numai valori pozitive” (negative).
La tine numitorul este
care al doilea şi al treilea factor au semne constante, -, respectiv +.Dar, în orice vecinătate a lui 0, factorul x ia şi valori pozitive
şi valori negative, deci nu poţi scrie nici +0, nici -0. Totuşi, dacă ”omisiunea” de care vorbeşti se referă la intervalul [0; 0,1), atunci poţi
să scrii ”+0”, dar asta înseamnă că tu calculezi limita la stânga.
În general, când calculezi limita la stânga în a, consideri x<a, tocmai pentru a ”omite” valorile pe care le-ar lua numitorul atunci când
Cu bine, ghioknt.
Tu ai încredere în relaţia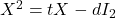
? (Cayley) Sau crezi că e o păcăleală şi nu ai folosit-o niciodată. Cu t am notat urma 
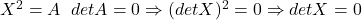. Relaţia lui Cayley devine:
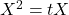, de unde tX=A. Ridicăm la pătrat ambii membri şi obţinem 
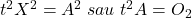relaţie posibilă numai dacă 
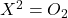care contrazice relaţia din ipoteză.
matricei X şi cu d determinantul ei.
Fie A matricea dată. Din
t=0; dar atunci relaţia lui Cayley devine
Cu bine, ghioknt.
[quote=ghioknt]Tu ai încredere în relaţia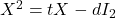
? (Cayley) Sau crezi că e o păcăleală şi nu ai folosit-o niciodată.
Cred ca este o pacaleala !!🙂 ))
Ps: Multumesc pt rezolvare.