radical x+ 1 +radical x +6 =5 /()la a 2
x+1>0
x>-1
x apartine [-6;+infinit)
x+6>0
x>-6
x+1+x+6=25
2x=25-7
2x=18
x=9
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Mai întâi, apreciez faptul că te străduieşti să rezolvi exerciţiile, spre deosebire de alţii, majoritatea, care doar întreabă. Aşa că cei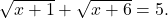 Este foarte bine să pui la început condiţiile de existenţă, atunci când ecuaţia conţine 2 sau
Este foarte bine să pui la început condiţiile de existenţă, atunci când ecuaţia conţine 2 sau . Ai două opţiuni: să rezolvi, sau să nu rezolvi sistemul de inecuaţii. Să zicem că nu-l rezolvi.
. Ai două opţiuni: să rezolvi, sau să nu rezolvi sistemul de inecuaţii. Să zicem că nu-l rezolvi.
 .
. are 3 termeni:
are 3 termeni:  ). Este nevoie de încă o ridicare la pătrat; numai că acum membrul II
). Este nevoie de încă o ridicare la pătrat; numai că acum membrul II cu precedenta ci doar în relaţia
cu precedenta ci doar în relaţia  , adică noua ecuaţie poate
, adică noua ecuaţie poate , fie verificându-le în ecuaţia originală. Aşadar:
, fie verificându-le în ecuaţia originală. Aşadar:
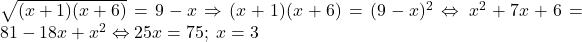 .
.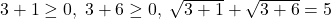
care îţi răspund văd ce ştii şi ce nu ştii şi pot să-ţi dea exact ajutorul de care ai nevoie.
Ecuaţia este
mai mulţi radicali:
Dacă ridici la pătrat ecuaţia aşa cum este acum, ai avantajul că ambii membri sunt pozitivi, deci obţii o ecuaţie ehivalentă cu cea dată:
(Aici ai greşit:
nu are numai valori pozitive. Noua ecuaţie nu mai poate fi în relaţia
avea rădăcini în plus. Le depistăm, fie supunându-le la testul
Acest 3 verifică condiţiile de existenţă (pe care nu le-am rezolvat) şi ecuaţia originală:
care sunt toate adevărate.
Dacă alegi să rezolvi inecuaţiile, intersectezi cele 2 soluţii şi obţii domeniul de existenţa [-1; oo); la final verifici că 3 aparţine intervalului.
Cu bine, ghiolnt.