lim n^2(a^1/n + a^1/n+1) eu am obtinut 0 ,as dori sa stiu daca am obtinut rezultatul corect
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
lim n^2(a^1/n + a^1/n+1) eu am obtinut 0 ,as dori sa stiu daca am obtinut rezultatul corect
Asa dupa cum ai scris a^(1/n)->1 .La fel i a^(1/(n+1))->1 ,
( n^2)(a^(1/n)+a^(1/(n+1)))=(n^2).2->infinit.
de ce 0??
este – acolo pt a fi nedeterminare 00*0
Rezolvarea mea arata in modul urmator:
lim n^2[a^1/n-1-(a^1/(n+1) -1) am fortat sa apara la jos 1/n iar la a doua 1/n+1 si am obtinut lim n^2(lna/n+lna/(n+1)) =lin nlna -n^2lna/(n+1)=lim nlna -nlna(1+1/n) si am cosiderat ca 1+1/n tinde la 1 si am obtine nlna-nlna=0,lim 0=0
Ai făcut în mod repetat o greşeală pe care eu aş numi-o ”trecerea la limită sub limită”. Să urmarim calculele tale.
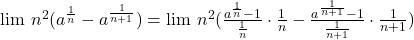. Ca să poţi să înlocuieşti cele 2 rapoarte cu limitele lor, lna, trebuie să treci la limită, adică să distribui limita termenilor, factorilor, bazelor şi exponenţilor etc, cf. regulilor învăţate pentru operaţii cu limite. Corect ar fi fost
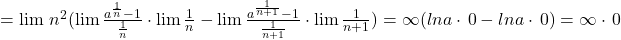. Tu cum ai făcut? Ai trecut la limită unde ţi-a convenit, apoi ai retras limita la loc, în faţă?
Cu bine, ghioknt.