A=(cos^2 x sin^2 x
sin^2 x cos^2 x )
A^n=?
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Matricea A este de forma A=aI+bJ, unde a=cos^2x, b=sin^2x,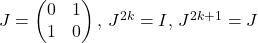
., iar I si J comută între ele, deci putem aplica binomul lui Newton.
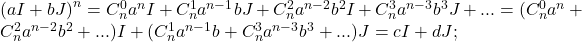
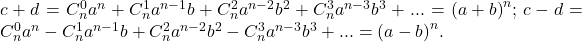
![c=\frac{1}{2}[{(a+b)}^n+{(a-b)}^n]=\frac{1}{2}(1+{cos^n2x),\,d=\frac{1}{2}[{(a+b)}^n-{(a-b)}^n]=\frac{1}{2}(1-{cos^n2x).](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-06a1e1d97985effe0805b2be5d43f34b_l3.png "Rendered by QuickLaTeX.com")
.
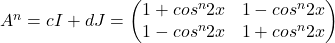Adunând şi scăzând aceste relaţii, obţinem:
Cu bine, ghioknt.
Domnule PhantomR, această postare a fost scrisă fără ”cârje”. Incă odată vă mulţumesc!