Home/ Intrebari/Q 83556
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

MDCristi
Pe: 2013-10-22T18:48:09+03:00 In: In:

limite laterale

As avea si eu nevoie de un indiciu, am rezolvat acest exercitiu dar nu sunt sigur daca l-am facut bine. Mi-ar prinde bine nu o rezolvare ci o descriere succinta a modului in care l-ati rezolva voi, intrucat nu am inteles atat de bine principiul de rezolvare al acestor exercitii.

Cerinta: Sa se calculeze limitele laterale ale functiilor de mai jos in punctele indicate.
$f:R->R, f(x) = \begin{cases} \frac{1}{1+2^\frac{1}{x-3}} & x \neq 3\\ 3 & x = 3 & \end{cases}in\: a = 3 $

Similare

1 raspuns

  1. xor_NTG
    maestru (V)

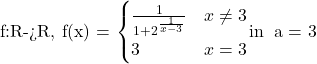
    Calcularea limitelor laterale a unei functii intr-un punct dat nu este o sarcina extrem de complexa. Sunt necesare insa cateva lucruri de baza in vederea indeplinirii ei.

    Avem functia:

    *** QuickLaTeX cannot compile formula:
\[
	\begin{array}{l}
	 f]
	

*** Error message:
\begin{array} on input line 9 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 9 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Emergency stop.

    Trebuie sa calculam limitele laterale (asta inseamna sa calculam limita laterala la dreapta si limita laterala la stanga).

    Limita laterala la stanga in punctul x = 3 se noteaza asa:

        \[ {\lim }\limits_{ x \to 3 \hfill \atop x < 3 \hfill} f\left( x \right) \]

    sau asa:

        \[ {\lim }\limits_{x \uparrow 3} f\left( x \right) \]

    (de fapt acea sageata este oblica indreptata spre dreapta si nu verticala cum am facut-o eu).

    O limita laterala intr-un anumit punct arata comportarea functiei in vecinatatea punctului respectiv (daca functia tinde spre o valoare reala sau spre infinit).

    Pe cazul de fata:

        \[ {\lim }\limits_{x \uparrow 3} f\left( x \right) = {\lim }\limits_{x \uparrow 3} \frac{1}{{1 + 21x - 3}} = \frac{1}{{ - 2 + 63}} = \frac{1}{{61}} \]

    Am intrat pe prima ramura a functiei deoarece se calculeaza limita functiei atunci cand x tinde catre 3 si este mai mic decat 3 (pentru ca avem limita laterala la stanga) deci x-ul nostru nu este egal cu 3, astfel incat sa putem intra pe ramura a 2-a.

    Limita laterala la dreapta este exact ca aceasta numai ca se schimba semnul relational de sub limita. Valoarea limitei este aceeasi (de aceasta data x-ul tinde catre 3, dar este mai mare, pentru ca avem limita la dreapta).

    Singurele „probleme” care pot aparea atunci cand se calculeaza limitele laterale sunt acelea in care trebuie calculata limita dintr-o functie rationala care la inlocuirea variabilei cu valoarea punctului la care tinde x-ul, obtinem la numitor 0.

    De exemplu

    Sa se calculeze

        \[ {\lim }\limits_{x \to 2} \frac{{15}}{{x - 2}} \]

    Observi ca daca inlocuiesti direct cu 2, obtii la numitor 0, ceea ce nu exista.

    Calculam deci limitele laterale sa vedem cum se comporta functia in vecinatatea acestei valori:

        \[ {\lim }\limits_{ x \to 2 \hfill \atop x < 2 \hfill} \frac{{15}}{{x - 2}} = \frac{{15}}{{0_ - }} = - \frac{{15}}{{0_ + }} = - \infty \]

    Explicatia: avem de calculat acea functie. Limita laterala la stanga presupune ca x-ul nostru tinde catre 2, dar este mai mic ca 2. Poti sa ti-l imaginezi ca fiind 1.999999999999999…98 si el tot se mareste incercand sa ajunga spre 2, dar nu il ajunge.

    Daca noi scadem din acest numar x, pe 2 (valoare fixa, constanta), obtinem un numar foarte apropiat de zero, dar negativ, ceva de genul -0.00000000000000000000…01. Acest numar se scrie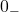 0_ -

    Ei bine, ducem minusul in fata fractiei si obtinem 15 supra 0.0000000000…01. Acest numar foarte apropiat de zero, dar pozitiv (ceea ce inseamna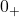 0 _ +, poate fi scris ca 1 supra un numar foarte mare (poti sa ti-l imaginezi ca 1 supra 10000000….0000…).

    Deci, la nivel conceptual, fractia noastra devine:

        \[ - \frac{{15}}{{0_ + }} = - \frac{{15}}{{\frac{1}{{10000...000}}}} = - 15 \cdot 10000...000 = - \infty \]

    . Este egal cu infinit, pentru ca nu avem nici un fel de apreciere legata de cuantumul acelei apropieri (numarul ala poate avea zeci de milioane de zerouri, deci se considera ca fiind infinit).

    In mod similar se calculeaza si limita la dreapta.

    Sper ca ai inteles ceva.

Raspunde

Raspunde