Daca a,b,c>=0 si a^2+b^2+c^2=3 aratati ca (a^2+a+1)(b^2+b+1)(c+2+c+1)<=27
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Salut,
Pentru a rezolva problema avem nevoie de următoarele inegalităţi: Mg3 <= Ma3 <= Mp3, unde Mg3 este media geometrică a 3 numere pozitive, Ma3 este media aritmetică a 3 numere pozitive şi Mp3 este media pătratică a 3 numere pozitive.
Aplicăm această treabă pentru numerele pozitive a^2+a+1, b^2+b+1 şi c^2+c+1, mai întâi partea legată de Mg3 <= Ma3:
Relaţia (1):
![\bl\sqrt[3]{(a^{\small 2}+a+1)\cdot(b^{\small 2}+b+1)\cdot(c^{\small 2}+c+1)}\le\frac{(a^{\small 2}+a+1)+(b^{\small 2}+b+1)+(c^{\small 2}+c+1)}{3}=\frac{a^{\small 2}+b^{\small 2}+c^{\small 2}+a+b+c+3}{3}=\frac{3+a+b+c+3}{3}=\frac{6+a+b+c}{3}=\\=2+\frac{a+b+c}{3}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-7fddf3d387215cd12eece04beba161d2_l3.png "Rendered by QuickLaTeX.com")
Apoi, aplicăm Ma3<=Mp3 pentru numerele pozitive a, b şi c:
Deci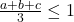
=> 
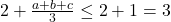(2)
Din relaţiile (1) şi (2) rezultă că:
Egalitatea are loc pentru a = b = c.
Green eyes.