Sa se calculze:
![\lim_{n\to \infty} \frac{1\cdot2\cdot3\cdot4+2\cdot3\cdot4\cdot5+...+n(n+1)(n+2)(n+3)}{[1\cdot3+2\cdot4+...+n(n+2)]\cdot [2^2+4^2+...+(2n)^2]}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-5aaae6c103214430e247841897067e3b_l3.png "Rendered by QuickLaTeX.com")
Multumesc.
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Salut,
Gradul polinomului de la numărător este 4, la fel şi la numitor, deci limita este egală cu câtul dintre coeficienţii determinanţi, adică împărţirea dintre coeficientul lui n la puterea cea mai mare de la numărător şi coeficientul lui n la puterea cea mai mare de la numitor.
La numărător avem sumă pentru k= 1, 2, 3, …, n pentru:
Având în vedere observaţiile de mai sus, ne interesează coeficientul lui n la puterea cea mai mare, din sumă de la 1 la n din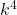
. Ştim că:
Pentru numitor avem termenul general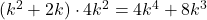
, deci ne interesează coeficientul lui n la puterea cea mai mare pentru:
Împărţim rezultatele de la (1) şi (2) şi obţinem: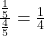
, acesta este rezultatul final.
Green eyes.
La inceput aplicamteoria Stiltz – Cezaro (conditia este ca numitorul limitei sa tinda la infinit cand n-> la infinit
L=lim(n->infinit)An/Bn=lim(n->infinit)(A(n+1)-An)/(B(n+1)-Bn)=(n+1)(n+2)(n+3)(n+4)/[(M+(n+1)(n+3))(N+(2(n+1))^2)-M.N], unde M=1.3+2.4+3.5+……+n(n+2) si N=2^2+4^2+6^2….+(2n)^2.Sumele M si N se pot scrie si mai restrans ;N=2^2[1^2+2^2+3^2+….n^2)=4.n(n+1)(2n+1)/6=2n(n+1)(2n+1)/3
M=1^2+2^2+3^2+…n^2+2(1+2+3…+n)=n(n+1)(2n+1)/6 + n(n+1)=
n(n+1)(2n+7)/6.
Deci L=(n+1)(n+2)(n+3)(n+4)/[n(n+1)(2n+7).4(n+1)^2/6+2.n(n+1(2n+1)(n+1)(n+3)/3+4(n+1)^3(n+3)]. Cum gradul numaratorului este 4 si gradul numitorului este 5, cand n->infinit L->0