Va rog frumos ..daca puteti sa imi aratati cum se fac sirurile astea…trb sa arat monotonia si marginirea lor. Am nevoie de ele …Va multumesc mult anticipat .
1) xn= 1/(1*2)+1/(2*3)+…+1/(n-1)n
2) xn=1+1/(2**alfa) +1/(3**alfa)+…+1/(n**alfa) , alfa apartine {2,3}
1/(2**alfa) = 1 supra (2 la puterea alfa)


NOTA: La sirul de la exercitiul 1 o sa imi asum ca primul termen este deoarece
deoarece  nu prea ar avea sens.
nu prea ar avea sens.
Pentru ambele: Monotonia e usoara, trebuie sa faci doar diferenta dintre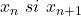
La 1 vei obtine :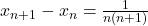 si deoarece diferenta e pozitiva(1 e pozitiv si produsul
si deoarece diferenta e pozitiva(1 e pozitiv si produsul 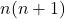 e pozitiv) sirul e strict crescator.
e pozitiv) sirul e strict crescator.
La 2: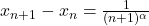 , pozitiv, la fel ca mai sus deci si acest sir este strict crescator.
, pozitiv, la fel ca mai sus deci si acest sir este strict crescator.
Cand un sir este strict crescator marginea inferioara este primul termen deci:
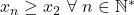
Pentru marginea superioara:
1)Voi incepe cu urmatoarea egalitate:
Daca rescriem adunarea dupa formula asta avem:
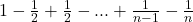
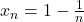 care e mai mic decat 1.
care e mai mic decat 1.
Dupa cum se observa, inafara de primul si ultimul pentru fiecare termen pozitiv exista un opus iar suma lor este 0, astfel suma va ajunge
Avem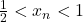 .
.
2)Pentru inceput voi rescrie sirul:
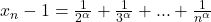
 este in multimea {2,3} cea mai mica valoare a lui
este in multimea {2,3} cea mai mica valoare a lui  va fi 2 deci cea mai mare valoare a sirului de mai sus va fi:
va fi 2 deci cea mai mare valoare a sirului de mai sus va fi:
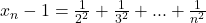
Deoarece
Asta e valoarea pentru care trebuie sa gasim o margine superioara.
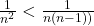
Vom folosi urmatoarea inegalitate:
Daca le punem unele sub altele avem:
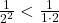
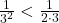

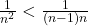
Daca adunam inegalitatile vom obtine:
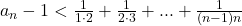
Rezolvarea sirului din dreapta inegalitatii se face ca la exercitiul anterior si cum acesta este mai mare decat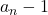 marginea lui va fi compatibila pentru a fi marginea lui
marginea lui va fi compatibila pentru a fi marginea lui 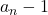 .
.
Vom avea: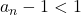 deci
deci 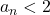 .
.
Restul calculelor si concluziilor cred ca le poti face/trage singura.
multumesc mult🙂