PROBLEMA 1 : Sa se demonstreze ca : 10 + √24 + √40 + √60 (toate sub un radical) = √2 + √3 + √5
PROBLEMA 2 :.Sa se scrie numarul √(de ordin 3) 9√3 – 11√2 sub forma a√2 + b√3 cu a,b apartin Q.
PROBLEMA 3 :.Sa se arate ca numarul A este rational :
A = √ 26+6√13-4√8+2√6-2√5(toate sub primul radical) + √26-6√13+4√8-2√6+√5(toate sub primul radical)
PROBLEMA 4 :Sa se determine multimile de numere :
A = {x € N / √12/x+3(toate sub un radical,si este o fractie) €N}.
B = {x € N / √(de ordin 3) 54/x-2 toate sub un radical,si este o fractie) €N}
O zi buna![/code]


Salut,
Să vedem:
Problema 1:
Ştim că:
Pentru a respecta regulamentul, trebuie să trimiţi câte o încercare de rezolvare pentru fiecare problemă în parte.
În plus, de ce ai publicat 4 probleme la acelaşi subiect ? Ştiai că orice subiect trebuie să conţină o singură cerinţă, o singură problemă ?
Green eyes.
-Nu stiu cum se rezolva.
-Sunt 4 exercitii distincte,nu sunt un subiect.
Salut,
Da, corect, sunt 4 exerciţii distincte, deci ar fi trebuit să fi fost 4 subiecte separate ! Înţelegi ?
Green eyes.
Yup!
Acum, poti sa ma ajuti sau continuam cu off-topicul?
pentru ca trebuie ca
trebuie ca 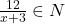
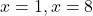 avem ca acel radical e patrat perfect.
avem ca acel radical e patrat perfect.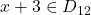
pentru
Ideea e sa verifici ca
apoi,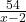 trebuie sa fie cub perfect,adica
trebuie sa fie cub perfect,adica 
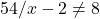 mai ramane ca
mai ramane ca  sau
sau 
cum
incearca la exercitiul 2 sa scrii mai explicit!
-In primul rand vreau sa-ti multumesc.Am sa incerc sa rescriu problema,dar nu stiu cum sa fac un radical de ordin 3.
am pus un tutorial de latex http://forum.matematic.ro/viewtopic.php?t=25658
Am rescris problemele :
1.Sa se scrie :
sub forma
2.Sa se arate ca numarul A este rational :
A = +
+ 
in ce priveste ultimul exercitiu


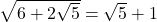
 asadar urmatorul radiccal e
asadar urmatorul radiccal e 
 si radical din acest numar este
si radical din acest numar este 

iar
trecem la urmatorul radical si avem
urmatoarea expresie de sub radical este
analog se arata ca celalalt radical,dupa multe calcule ,este
Multumesc!
avec plaisir comme toujours!