Home/ Intrebari/Q 82246
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

viperaza
Pe: 2013-07-10T14:43:26+03:00 In: In:

Numere complexe

Similare

8 raspunsuri

  1. TheodorMunteanu

    sigur in modulul din mijloc nu e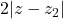 2|z-z_2|in looc de 2|z+z_2|?

  2. TheodorMunteanu

    din inegalitatea modulului |z-z_1|+|z-z_3|\geq |2z-(z_1+z_3)|=2|z-\frac{z_1+z_3}{2}|=2|z-z_2|
    deci 4|z|\geq 2|z-z_2|+2|z+z_2|\geq 2|z-z_2+z+z_2|=4|z|deci avem egalitate in prima inegalitate adica |z-z_1|+|z-z_3|=|2z-(z_1+z_3)|
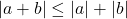    si avem |a+b|\leq|a|+|b|cu egalitate daca a=\alpha bunde alpha e real si pozitiv deci z-z_1=\alpha(z-z_3)

  4. viperaza

    Sigur 😀
    Daca am introduce acel 2 in modul şi am nota interioarele celor 3 moduli cu a, b si c atunci a+b+c ar fi egal cu 4z, data fiind relatia dintre z1, z2 s z3.

    Adica am avea ca: |a|+|b|+|c|=|a+b+c|
    si ar trebui sa demonstram ca a/c>0
    Poate ajuta aceasta observatie…

  5. viperaza

    Multumesc de rezolvare!

  6. TheodorMunteanu

    propun o problema asemanatoare cat de cat:
    daca \left|\frac{1}{z}-\frac{1}{2}\right|<\frac{1}{2}atunci Re z>1

  8. poseidon95

    cum aflu care e nr real din 1+3i/2+5i????????

  9. andu_flavius95
    maestru (V)

    poseidon95 wrote: cum aflu care e nr real din 1+3i/2+5i????????

    In primul rand ,este mai util daca ai deschide un topic nou pentru a primi un raspuns .

    Ai 2 metode la dispozitie :
    1 . Amplifici cu conjugata expresia data (in cazul tau , cu 2-5i) si tii cont de operatiile cu numere complexe si i^2=-1 ;
    z=Re(z)+i*Im(z)
    2 . Poti scrie sub forma trigonometrica doua numere z_1=1+3i ; z_2=2+5i si aplici formula:

        \[\frac{{{z_1}}}{{{z_2}}} = \frac{{{r_1}}}{{{r_2}}}\left( {\cos \left( {{t_1} - {t_2}} \right) + i\sin \left( {{t_1} - {t_2}} \right)} \right)\quad ,unde\;{z_k} = {r_k}\left( {\cos \left( {{t_k}} \right) + i\sin \left( {{t_k}} \right)} \right);k = \overline {1,2} .\]

  10. viperaza

    Pentru problema propusa de domnul Theodor Munteanu:

    fie z=r(cosx+isinx), deci Re(z)=rcosx

    1/z=1/r(cosx-isinx)

    |(cosx/r) – 1/2 – i(sinx/r)|=|2cosx – r – 2isinx|/2r<1/2

    De aici r^2 > (2cosx – r)^2 + (2sinx)^2 echivalent cu rcosx > (sinx)^2 + (cosx)^2=1, ceea ce trebuia demonstrat.

Raspunde

Raspunde