Azi am participat la barajul IMAC (Concurs ARHIMEDE). Sunt nesigur pe rezolvarile de la doua exercitii.
III.)
Pe un cerc se aleg punctele A, B si P. Din mijlocul M al arcului APB (nu ABP, nota mea!) este coborata perpendiculara MK pe cea mai mare dintre coardele AP si BP. Sa se demonstreze ca punctul K injumatateste linia franta APB.
II.) Iar al doilea arata cam asa:
*** QuickLaTeX cannot compile formula:
\[\begin{array}{l}
{\rm{Sa se determine numerele reale pozitive }}{x_1},{x_2},{x_3},...,{x_n},{\rm{ }}n \ge 2{\rm{ pentru care}} \\
\left\{ \begin{array}{l}
{x_1} + {x_2} + {x_3} + ... + {x_n} = \frac{3}{2} \\
\frac{1}{{{x_1} + {x_2}}} + \frac{1}{{{x_2} + {x_3}}} + ... + \frac{1}{{{x_{n - 1}} + {x_n}}} + \frac{1}{{{x_n} + {x_1}}} = 3 \\
\end{array} \right. \\
- - - - - - - - - - - - - - - \\
{\rm{Am mers pe varianta: 2}}\left( {{x_1} + {x_2} + {x_3} + ... + {x_n}} \right) = 2*\frac{3}{2} = 3 \Rightarrow 2{x_1} + 2{x_2} + 2{x_3} + ... + 2{x_{n - 1}} + 2{x_n} = \frac{1}{{{x_1} + {x_2}}} + \frac{1}{{{x_2} + {x_3}}} + ... + \frac{1}{{{x_{n - 1}} + {x_n}}} + \frac{1}{{{x_n} + {x_1}}} \\
\Rightarrow 2{x_1} + 2{x_2} + 2{x_3} + ... + 2{x_{n - 1}} + 2{x_n} - \frac{1}{{{x_1} + {x_2}}} - \frac{1}{{{x_2} + {x_3}}} - ... - \frac{1}{{{x_{n - 1}} + {x_n}}} = \frac{1}{{{x_n} + {x_1}}} \Rightarrow {x_1} + \underbrace {{x_1} + {x_2} - \frac{1}{{{x_1} + {x_2}}}}_{} + \underbrace {{x_2} + {x_3} - \frac{1}{{{x_2} + {x_3}}}}_{} + ... + \underbrace {{x_{n - 1}} + {x_n} - \frac{1}{{{x_{n - 1}} + {x_n}}}}_{} + {x_n} = \frac{1}{{{x_n} + {x_1}}} \\
\Rightarrow \underbrace {{x_1} + {x_2} - \frac{1}{{{x_1} + {x_2}}}}_{} + \underbrace {{x_2} + {x_3} - \frac{1}{{{x_2} + {x_3}}}}_{} + ... + \underbrace {{x_{n - 1}} + {x_n} - \frac{1}{{{x_{n - 1}} + {x_n}}}}_{} + \underbrace {{x_1} + {x_n} - \frac{1}{{{x_n} + {x_1}}}}_{} = 0 \\
*** Error message:
\begin{array} on input line 10 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 10 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Emergency stop.
Multumesc anticipat!


Salut,
O sugestie pentru exerciţiul II:
Ar fi trebuit să te fi folosit de inegalitatea dintre media aritmetică şi cea armonică, adică:
(a1 + a2 + … + an) / n >= n / (1/a1 + 1/a2 + … + 1/an), (1), luând aşa:
a1 = 1/(x1 + x2), a2 = 1/(x2 + x3), …, an = 1/(xn + x1).
Înlocuind cu datele din enunţ ai fi obţinut că:
3/n >= n/3, apoi după rezolvarea inecuaţiei (ştiind că n >=2) ai fi obţinut că n = 2 sau n = 3.
Pentru n = 2, rezultă că 3/2 = 2/3 – absurd.
Pentru n = 3, rezultă că:
1/(x1 + x2) + 1/(x2 + x3) + 1/(x3 + x1) = 3 şi x1 + x2 + x3 = 3/2
Dar povestea asta este chiar cazul de egalitate a celor 2 medii (aritmetice şi armonice), pentru inegalitatea (1) de mai sus, cu termenii 1/(x1 + x2), 1/(x2 + x3) şi 1/(x3 + x1).
Egalitatea are loc dacă termenii sunt egali, adică 1/(x1 + x2) = 1/(x2 + x3) = 1/(x3 + x1) => x1 = x2 = x3 = 1/2.
Sper să te fi ajutat. Mult succes !
Green eyes.
la aceeasi problema se poate folosi si inegalitatea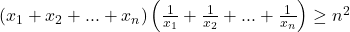 iar aici trebuia rescrisa prima egalitate ca
iar aici trebuia rescrisa prima egalitate ca 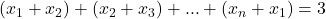 si aveam ca
si aveam ca 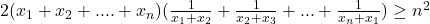 deci ar fi rezultat ca
deci ar fi rezultat ca 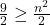 deci
deci 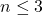 si pe de alta parte se respecta cazul de egalitate.
si pe de alta parte se respecta cazul de egalitate.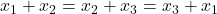 etc.
etc.
cand