Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Salut.
Am si eu o problema , care nu stiu sa o rezolv.
Se considera o functie f definita pe R cu valori in R. f(x) este radical din 1-x daca x <=1, respectiv 1-x, daca x> 1.
Sa se arate ca f este inversibila.
Sa se traseze graficul functiei f.
Eu stiu sa demonstrez ca este bijectiva daca am doar o expresie. Cum rezolv problema asta?
Multumesc, si sa aveti o zi faina!
f(x)=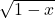
x<,=1 (A)
1-x x>1 (B)
Suerjectivitaatte caz1 X<,=1 fie y e R+ a.i y==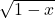
y^2=1-x =>x=1-y^2 aceasta reprezita o functiee de grd 2 inn y cu
a=-1, b=0, c=1 SE STIE CA FUUNCTILLE De gr 2 sun surjectiive pe intervale de forma (-oo, -b/2a] sii [-b/2a,+oo)In caazul tau -b/2a=0
DECI PT Y E [, +oo) xe ((-oo, 1] Surjectivitatea e ddemonstrata la (A)
Caz B AIci ai funcctie d grd 1definita ppe submultimme a luui R. Se stie ca functiiile de gd 1sunt srjeectiveDeci f(x) este surjecivva pe R
=
Ridici l patrat si obtii
IInjectivitatea CAZ (A)) xe (-oo, 1] presuppui ca f nu e injectiva Fie X1<X2<1 a.. f(x1=f(x2) deci
1-x1=1-x2 adica x1=x2 . deci f (x1)=f(x2) implica X1=X2 Dei f eesyte injectiva pe (-oo, 1]
Cazul B Xe [1,, +oo))funtia de ggrd 1 ese inectiva pe R
ESTE NJECTIVA PE R
CCaz C x1e (-oo, 1],, x2 e [1, +00) f(x1)=f(x2)
Observa c membul drept e poztiv si membrul drept ee negativ.Eegalitate imposibila, Ddcci f este injectiva =>….