Home/ Intrebari/Q 79931
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

cosmin_k
Pe: 2013-01-16T18:27:45+02:00 In: In:

2 limite

sa se calculeze:

    \[\begin{array}{l} {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} - \sqrt[3]{{x + 1}}}}{x} \\ {\lim }\limits_{x \to 0} \frac{{2^x + 3^x + 4^x - 3}}{{5^x + 6^x + 7^x - 3}} \\ \end{array}\]

Similare

5 raspunsuri

  1. xor_NTG
    maestru (V)

    La primul aplici formula conjugatei de grad III: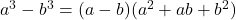 a^3-b^3=(a-b)(a^2+ab+b^2)

    La al doilea dai factor fortat sus pe 4 la x iar jos pe 7 la x. Vezi ce iese.

  2. cosmin_k

    nu prea merge la a) asa 😕

  4. ali
    maestru (V)

    Problema 2 mai interesanta:
    {\lim }\limits_{x \to 0} \left( {\frac{{{2^x} + {3^x} + {4^x} - 3}}{{{5^x} + {6^x} + {7^x} - 3}}} \right) = {\lim }\limits_{x \to 0} \frac{{\frac{{{2^x} - 1}}{x} + \frac{{{3^x} - 1}}{x} + \frac{{{4^x} - 1}}{x}}}{{\frac{{{5^x} - 1}}{x} + \frac{{{6^x} - 1}}{x} + \frac{{{7^x} - 1}}{x}}} = \frac{{\ln 2 + \ln 3 + \ln 4}}{{\ln 5 + \ln 6 + \ln 7}} = \frac{{\ln \left( {24} \right)}}{{\ln \left( {210} \right)}}
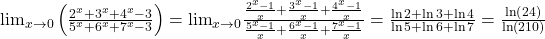
    Subtil … dar nu prea!!!! 🙂

  5. ex-admin
    profesor

    O alta ideea la a):

        \[ {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} - \sqrt[3]{{x + 1}}}}{x} = {\lim }\limits_{x \to 0} \left( {\frac{{\sqrt {x + 1} }}{x} - 1} \right) + {\lim }\limits_{x \to 0} \left( {1 - \frac{{\sqrt[3]{{x + 1}}}}{x}} \right)\]

  6. DD
    profesor

    Attached files

Raspunde

Raspunde