Am o listă cu probleme de la grupul de excelenţă printre care sunt câteva care nu îmi ies şi vă rog să-mi săriţi în ajutor.
1. Fie z1, z2 numere complexe astfel încât lz1+z2l=lz1l=lz2l=1.
Să se determine toate numerele n naturale nenule cu proprietatea că (z1)^n=(z2)^n.
2.Fie z1, z2, z3 numere complexe nenule. Să se demonstreze că dacă z1+z2+z3 = z1z2 + z2z3 + z1z3 = 0 atunci lz1l=lz2l=lz3l.
3.Fie x, y, z complexe nenule distincte două câte două astfel încât x + (1\y) = y + (1\z) = z + (1\x). Demonstraţi că xyz este număr real de modul 1.
4.Fie a> 1\2 şi mulţimile A={z complexe| lzl>=a}, B={z complexe| |z-1-i|<=2a}. Arătaţi că |Re(z)-Im(z)| <= a*radical(2) pentru oricare z aparţine A intersectat cu B.
5.Fie a real şi z complex astfel încât a=|z+ (1\z)|. Să se determine cea mai mare şi cea mai mică valoare a lui |z|.
6.Fie z1, z2 complexe nenule a.î. |z1+z2|=|z1|=|z2|. Să se calculeze z2\z1.
7.Demonstraţi că dacă z e un număr complex cu |z^4 + 2| = |z^2| atunci |z|<=radical(2).
8.Dacă z şi a sunt numere complexe |z|=1 şi n e un număr natural nenul să se arate că |z+a| + |(z^2) + a| +…+ |(z^2n) + a| >= n*|z-1|.
9.Fie k,n naturale nenule şi z1, z2,…,zn complexe nenule cu acelaşi modul şi z1^k + z2^k + … + zn^k = 0, să se arate că 1\z1^k + 1\z2^k +…+ zn^k = 0
10.Fie z un număr complex cu modulul 1. Să se arate că: n|1+z| + |1+z^2| +…+|1+z^(2n+1)| >= 2n.
11.Fie z1, z2, z3, z4 numere complexe cu module egale şi z1+z2+z3+z4=0. Arătaţi că pentru orice n natural impar are loc egalitatea: 1\z1^n + 1\z2^n + 1\z3^n + 1\z4^n = 0.


Citeste regulamentul forumului❗
P 2
Fiie ecuatia de grd in z
aZ^3+bZ^2+CZ+d=0 Imparrti reltia cu a=/=0
Z^3+b/aZ^2+c/aZ+d/a=0
CConf reelatiilor lui Viette b/a=c/a=0
Z^3+t=0 pt usurinta calculellor am pus d/a=t Ecatiia se mai scrie
(Z+t)*(Z^2-tz +t^2)=0
Z+t=0 Z1=-t IZ1I=I-tIt=t
z2=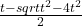 =
=![Rendered by QuickLaTeX.com \frac{t-ti[tex]\sqrt{3}}{2}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-34c42c65903e5ef47d42f4c3309b88b1_l3.png)
IZ2I=t
Analog clcuulezi Z3 SI DETERMINI IZ3I=t
1.
Avem
Folosind (*1), primim
Fie
, si primim
Deoarece avem |z1|=|z2|=1, primim
Stim ca
, deci egalitatea
este echivalenta cu
Din (*2), primim
Daca
Stim ca
, deci avem
Folosim formula de Moivre, si primim
Se vede, ca pentru orice n=3k avem
, deci am terminat.
In concluzie, egalitatea (z1)^n=(z2)^n are loc (numai) pentru n-urile de forma 3k.
* Poate voi mai trimite rezolvari si la alte probleme, insa ar fi bine sa scrii si tu ceea ce ai reusit sa faci.
** Consider ca o lista cu 11 probleme intr-un singur subiect este mult…
Mulţumesc pentru rezolvări. Pentru rezolvarea lui sandy_sc de la problema 2 trebuie să studiez teoria pentru relaţiile lui Viete la polinoame.
Rezolvarea la problema 1 mi se pare interesantă.
Îmi cer scuze că nu am citit mai întâi regulamentul. Dacă e necesar le voi scrie pe toate separat.
Da, aşa este, e o rezolvare frumoasă. (după ce am aflat relaţiile lui Viete la ecuaţia de gradul 3)
Dar am o întrebare totuşi. Orice numere complexe pot fi rădăcini ale unei ecuaţii de gradul 3?
Pentru că în cazul ecuaţiei de gradul 2, rădăcinile sunt numere conjugate, deci au module egale. Iar pentru ecuaţia de gradul 3, dacă delta e mai mic decât 0 sunt două soluţii complexe conjugate (cu module egale) şi una reală
Observatia ta e valabila pen tru ecuatii ccu coficieenti reali,Eu nu am precizzat natura numereloor a, b, c, d,Saa determin nr complex t nu am cnsiderat necesar intrucat t ie ti e cere lzl nu z