Home/ Intrebari/Q 79607
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

gunty
maestru (V)
Pe: 2012-12-21T13:35:57+02:00 In: In:

Ecuatie cu logaritm

Rezolvati ecuatia

    \[ x^{\log _a b} = x^2 - a^2 + b \]

unde a<1<b.

Ceea ce am reusit sa fac:

Deoarece 0<a<1 si b<1, inseamna ca

    \[ \log _a b < 0 \]

.
Deci egalitatea este echivalenta cu urmatoarea:

    \[ \frac{1}{{x^{\left| {\log _a b} \right|} }} = x^2 - a^2 + b \]

In cazul in care

    \[ x \in \left( {1; + \infty } \right) \]

:

    \[ \begin{array}{l} \Rightarrow x^{\left| {\log _a b} \right|} > 1 \Leftrightarrow \frac{1}{{x^{\left| {\log _a b} \right|} }} < 1_{(1)} \\ b - a^2 > 0_{(2)} \\ x^2 > 1_{(3)} \\ \end{array} \]

Din (1),(2),(3) rezulta ca pe acest interval egalitatea nu poate sa aiba loc, adica x apartine (0;1]

*Problema e de pe un alt forum. Mi s-a parut o problema interesanta, si sper ca rezolvarea sa fie la fel 😀.

Similare

10 raspunsuri

  1. DD
    profesor

    Ecuatia are o solutie unica X=a (Vezi ex. din fig)

  2. DD
    profesor

    Am reprezentat f(x)=(x^log(baza 0,2) din[ 3])-x^2+(0,2^2)-3

    Attached files

  4. gunty
    maestru (V)

    Intr-adevar x=a este solutie, dar cum s-ar putea demonstra ca e unica?

  5. GreatMath
    veteran (III)

    http://matematica-ajutor.forumz.ro/t748-ecuatie-logaritmica#2191 găsesti solutia completa si detaliata!
    Sper sa întelegi !

  6. gunty
    maestru (V)

    Imi cer scuze ca nu stiu, dar ce inseamna

        \[ \log \left( {a,b} \right) \]

    ? 😀

  8. GreatMath
    veteran (III)

    🙂)
    {\log _a}b = \log \left( {a,b} \right)

  9. PhantomR
    expert (VI)

    @GreatMath: Puteti folosi codul \LaTeX 

    \log_&#123;a&#125;&#123;b&#125;

    care va produce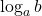 \log_{a}{b}.

  10. gunty
    maestru (V)

    Scrie asa:

        \[ a = \frac{m}{n},m < n \Rightarrow \log \left( {a,b} \right) = \log \left( {\frac{n}{m},b} \right) = ... \]

    Nu ar trebui in felul urmator?:

        \[ a = \frac{m}{n},m < n \Rightarrow \log \left( {a,b} \right) = \log \left( {\frac{m}{n},b} \right) = ... \]

  12. GreatMath
    veteran (III)

    Te-ai pierdut pe drum „boss de boss”
    \begin{array}{l} {x^{\log \left( {a,b} \right)}} = {x^2} - {a^2} + b \Rightarrow \log \left( {a,b} \right) = {\log _x}\left( {{x^2} - {a^2} + b} \right)\\ \log \left( {a,b} \right) = {\log _a}b = {\log _{\frac{m}{n}}}b = {\log _{{{\left( {\frac{n}{m}} \right)}^{ - 1}}}}b = - {\log _{\frac{n}{m}}}b\\ - {\log _{\frac{n}{m}}}b = {\log _x}\left( {{x^2} - {a^2} + b} \right) \Leftrightarrow {\log _{\frac{n}{m}}}b = - {\log _x}\left( {{x^2} - {a^2} + b} \right) = {\log _x}\frac{1}{{{x^2} - {a^2} + b}} \end{array}
    Rezolvarea este pur si simplu geniala !
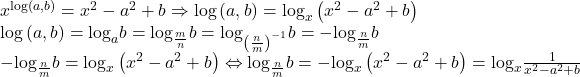
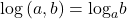    Iar despre \log \left( {a,b} \right) = {\log _a}b est o notatie internationala, nu o folosesc de fită (dacă întelegi ce vreau sa zic) ci ma ajuta enorm …. este în corelatie cu site-ul wolframe, ajuta la verificare!

  13. gunty
    maestru (V)

    Ca sa clarific, nu am nici o problema cu rezolvarea sau cu notatia. Ceea ce am intrebat, am facut-o pentru ca n-am inteles sau m-am blocat, nu pentru ca vreau sa subestimez munca ta sau al altcuiva. Multumesc pentru raspunsuri, si va doresc Craciun fericit 😀.

Raspunde

Raspunde