1. Sa se determine punctele de pe dreapta 3x+2y-12=0 situate la distanta 3 de dreapta 12x-5y+30=0.
2. Sa se scrie ecuatia unei drepte care trece prin punctul A(-2,0) si formeaza cu dreptele de ecuatii 3x-2y-7=0 si 2x+3y+4=0 un triunghi cu aria 13.
3. Se dau punctele A(3,2) ,B(6,4) si C(-2,2). Sa se determine locul geometric al punctelor M pt care A[MAB]=A[MBC] . (este vorba de arie -asa se noteaza in manual).
4. Fie A(a,b+1) ,B(a+1,b^2) ,C(1,1) ,a,b apartin Z si o multime M={N(a,b)| A,B,C sunt coliniare}.
a).Cate elemente are multimea M?
b).Sa se determine aria poligonului format de punctele din multimea M.
c).Studiati natura poligonului format de punctele multimii M.


Mai intai faci figura
DreaptA d 12X-5Y+30=0 trece prin punctele A(0,6) B(4,0)
dreapta d` :12X-5Y=30=0 trce prin punctele A(0,6) si C(2,5 , 0)
Fie M(x0,yo) si M`(X`,Y`) cele 2 puncte
Se aplica formula distantei de la un puncy M la dreapta d`
d(M,D`)=
*** QuickLaTeX cannot compile formula: \frac{laxo+byo+Cl}{sqrt{A^2+B^2} *** Error message: File ended while scanning use of \frac . Emergency stop.=3 (1)
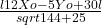 =3
=3
Faci inlocirile si obtii
Dar M se afla pe dreapta d Asadar ai relatia 3Xo+2yo-12=0 (2)
Din (1 si ( 2 ) obtii un sistem, Explicitezi modulul de la (1) si determini pe Xo,Yo si pe M`(x`, Y`)
Vei calcula aria dupa formula A!A2 A3 =determinantD/2
unde determinantul D =
X1 Y1 1
X2 Y2 2
X3 Y3 3 unde Xi, Yi sunt coordonatele punctelor A1 ,A2, A3
Aria Tr=MBA
XM Ym 1)l *1/2
3 2 1 l
6 4 1 l …=calcule=3/2YM-XM (1)
Aria tr m BC =
Xm YM 1 l *1/2
6 4 1 l
-2 2 1l = calcule=Xm-4YM+10 (2)
Mai revezi si tu calculele pt orice eventualitate
Egalezi relatiile 1 si 2 si obtii
XM-2YM+5=0 Deci locul geometric este dreapta de mai sus
Notezi cu d1 si d2 prima ,respectiv a2 a dreapta.Observi ca punctul A e d2.
Formezi sistem de ec cu d1 si d2 Punctul de intersectie al celor 2 drepte va fi un varf al triunghiului.
d1: 3x-2y-7=0
d2; 2x+3y+4=0
Rezolvi sistemul si aflii x=1 y=-2 Deci B(1, -2)
Aria tr ABC o determini cu formulela de la ex precedent
Aria (ABC)=
l -2 0 1l
l1 -2 1l
Xc yc 1 l*0.5=13. Inmultesti coloana 3 cu 2 si o aduni la col.1Vei obtine
l 0 0 1 l
l3 -2 1 l
lXc +2 Yc 1l* 0,5= calcule=>2Xc +3Yc-22=0Aceasta e dreapta care trece prin C.O intersectezi cu d1 pt a afla coordonatele punctului C
2x+3y=22
3x-2y=7 rezolvi si obtii X=1 Y=-4 Deci C =(1, -4)
Pt determinarea dreptei cerute te folosesti de relatia
Y-YA)/(YC-YA)=(X-Xa)/(XC-Xa) faci inlocuirile … continui tu
Pt ca punnctele respectie sa fie coliniar trebuie ca determminantul format de coodonattele l lor ssa fie nul