Home/ Intrebari/Q 79470
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

dennis9091
guru (IV)
Pe: 2012-12-11T12:26:07+02:00 In: In:

Inegalitate.

Daca a,b,c > 0 , sa se arate ca:

Attached files

def_466.doc (22 KB) 

Similare

7 raspunsuri

  1. ali
    maestru (V)

    Din păcate, metoda mea este un pic lunga însă foarte simpla ….:
    \begin{array}{l} {\left( {MA - MG} \right)_2}:\\ {\left( {a + b} \right)^2} \ge 4ab\\ {\left( {a + c} \right)^2} \ge 4ac\\ {\left( {a + b} \right)^2} + {\left( {a + c} \right)^2} \ge 4\left( {ab + ac} \right) \Leftrightarrow \frac{1}{{4\left( {ab + ac} \right)}} \ge \frac{1}{{{{\left( {a + b} \right)}^2} + {{\left( {a + c} \right)}^2}}}\\ {\rm{Idem}} \Rightarrow \frac{1}{4}\sum {\frac{1}{{ab + ac}}} \ge \sum {\frac{1}{{{{\left( {a + b} \right)}^2} + {{\left( {a + c} \right)}^2}}}} \\ {\left( {MA - MG} \right)_2}:\\ ab + ac \ge 2a\sqrt {bc} \Rightarrow \sum {\frac{1}{{ab + ac}}} \le \frac{1}{2}\sum {\frac{1}{{a\sqrt {bc} }}} \Leftrightarrow \frac{1}{4}\sum {\frac{1}{{ab + ac}}} \le \frac{1}{8}\sum {\frac{1}{{a\sqrt {bc} }}} \\ {\rm{Demonstrm ca}}\,\sum {\frac{1}{{{a^2}}}} \ge \sum {\frac{1}{{a\sqrt {bc} }}} \\ \sum {\frac{1}{{{a^2}}}} \ge \sum {\frac{1}{{a\sqrt {bc} }}} \Leftrightarrow \frac{{{{\left( {ab} \right)}^2} + {{\left( {bc} \right)}^2} + {{\left( {ca} \right)}^2}}}{{{{\left( {abc} \right)}^2}}} \ge \frac{{\sqrt {ab} + \sqrt {bc} + \sqrt {ca} }}{{abc}}\\ {\left( {ab} \right)^2} + {\left( {bc} \right)^2} + {\left( {ca} \right)^2} \ge abc\left( {\sqrt {ab} + \sqrt {bc} + \sqrt {ca} } \right)\\ {\left( {MA - MG} \right)_2}:\\ {\left( {ab} \right)^2} + {\left( {bc} \right)^2} \ge 2b \times abc \Rightarrow \sum {{{\left( {ab} \right)}^2}} \ge abc\sum a \\ {\rm{Demonstrm ca: }}abc\sum a \ge abc\sum {\sqrt {ab} } \Leftrightarrow \sum a \ge \sum {\sqrt {ab} } \to {\rm{Inegalitate arhicunoscuta!}} \end{array}

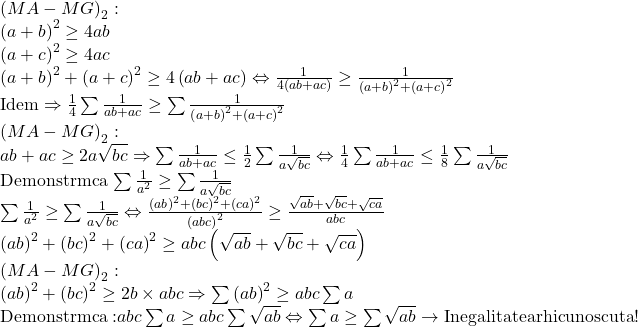
    Dupa cum vezi …. inegalitatea ta este una foarte slaba !

  2. dennis9091
    guru (IV)

    Iti multumesc mult

  4. dennis9091
    guru (IV)

    [quote=ali]Din păcate, metoda mea este un pic lunga însă foarte simpla ….:
    \begin{array}{l} {\left( {MA - MG} \right)_2}:\\ {\left( {a + b} \right)^2} \ge 4ab\\ {\left( {a + c} \right)^2} \ge 4ac\\ {\left( {a + b} \right)^2} + {\left( {a + c} \right)^2} \ge 4\left( {ab + ac} \right) \Leftrightarrow \frac{1}{{4\left( {ab + ac} \right)}} \ge \frac{1}{{{{\left( {a + b} \right)}^2} + {{\left( {a + c} \right)}^2}}}\\ {\rm{Idem}} \Rightarrow \frac{1}{4}\sum {\frac{1}{{ab + ac}}} \ge \sum {\frac{1}{{{{\left( {a + b} \right)}^2} + {{\left( {a + c} \right)}^2}}}} \\ {\left( {MA - MG} \right)_2}:\\ ab + ac \ge 2a\sqrt {bc} \Rightarrow \sum {\frac{1}{{ab + ac}}} \le \frac{1}{2}\sum {\frac{1}{{a\sqrt {bc} }}} \Leftrightarrow \frac{1}{4}\sum {\frac{1}{{ab + ac}}} \le \frac{1}{8}\sum {\frac{1}{{a\sqrt {bc} }}} \\ {\rm{Demonstrm ca}}\,\sum {\frac{1}{{{a^2}}}} \ge \sum {\frac{1}{{a\sqrt {bc} }}} \\ \sum {\frac{1}{{{a^2}}}} \ge \sum {\frac{1}{{a\sqrt {bc} }}} \Leftrightarrow \frac{{{{\left( {ab} \right)}^2} + {{\left( {bc} \right)}^2} + {{\left( {ca} \right)}^2}}}{{{{\left( {abc} \right)}^2}}} \ge \frac{{\sqrt {ab} + \sqrt {bc} + \sqrt {ca} }}{{abc}}\\ {\left( {ab} \right)^2} + {\left( {bc} \right)^2} + {\left( {ca} \right)^2} \ge abc\left( {\sqrt {ab} + \sqrt {bc} + \sqrt {ca} } \right)\\ {\left( {MA - MG} \right)_2}:\\ {\left( {ab} \right)^2} + {\left( {bc} \right)^2} \ge 2b \times abc \Rightarrow \sum {{{\left( {ab} \right)}^2}} \ge abc\sum a \\ {\rm{Demonstrm ca: }}abc\sum a \ge abc\sum {\sqrt {ab} } \Leftrightarrow \sum a \ge \sum {\sqrt {ab} } \to {\rm{Inegalitate arhicunoscuta!}} \end{array}

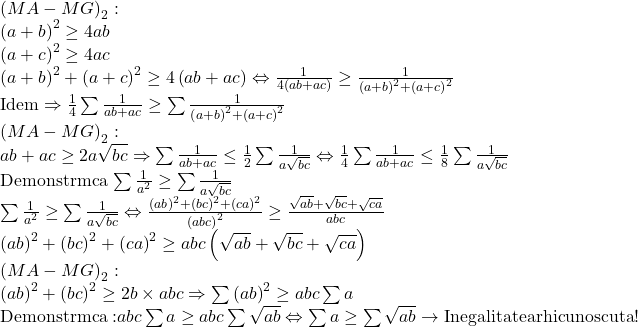
    Revin la acest exercitiu. Am stiudiat rezolvarea ta cateva zile.. Si am descoperit ca nu e o rezolvare corect 100%. unde spui ca trebuie demonstrat ca 1/(a radical din bc ) > 1/a^2 … ar trebui sa restrangi inegalitatea si se demonstrezi ca 1/(a radical din bc ) < 1/a^2.. membrul stang se poate afla intre membrul drept si 1/(a radical din bc) + 1/(b radical din ac) + 1/(c radical din ab) …

  5. ali
    maestru (V)

    Si am descoperit ca nu e o rezolvare corect 100%


    Nu am înteles ce vrei sa spui …. as prefera dacă ai folosi codul latex sa înteleg unde anume am gresit !
    M-am uitat încă odată pe rezolvare …. este una foarte simpla …. nu pare sa fie nimic gresit …. pur si simplu MA-MG consecutive!

  6. edy8
    maestru (V)
    ..
  8. Anonim99

    Dennis, rezolvarea imi pare corecta, se demonstreaza prin inegalitati succsive.
    Succes la judeteana!

  9. dennis9091
    guru (IV)

    Iti multumesc. Sa fie.. Chiar sunt curios sa vad ce vor da..

Raspunde

Raspunde