Aflati numerele reale x si y astfel incat:
8x^2+y^2-4xy+8x-2y+2=0.
(PS. am incercat sa fac (a+b+c)^2 , dar nu mi’a iesit )
dennis9091guru (IV)
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Aflati numerele reale x si y astfel incat:
8x^2+y^2-4xy+8x-2y+2=0.
(PS. am incercat sa fac (a+b+c)^2 , dar nu mi’a iesit )
Privesti problema dintr-un unghi gresit …. inteligent ar fi:
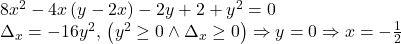
Nu prea inteleg rezolvarea.. nu stiu de unde delta aia.. (ps. cunosc ecuatia de gradul 2)…
Pai am grupat ecuatia după x => o ecuatia de gradul 2 în x toate celelalte variabile (în acest caz numai y) ce apar în ecuatie sunt coeficienti a lui x sau termeni liberi ….. în rest, se calculează delta (s-a notat si coeficientul ca sa-ti dai seama despre ce delta este vorba, de exemplu puteai la fel de frumos sa calculezi si delta după y)…..
Nu cred ca exista o solutie mai frumoasa si mai simpla ca asta !