Daca intr-un triunghi dreptunghic ABC cu m(A)=90 avem AB+AC>=2, atunci BC>=radical din 2
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Daca intr-un triunghi dreptunghic ABC cu m(A)=90 avem AB+AC>=2, atunci BC>=radical din 2
O posibila solutie (un pic mai lunga) ar fi :
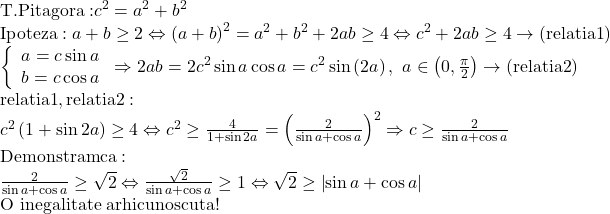
Sau:
b+c>=2 de unde rezulta, aplicand Mp>=Ma>=1 (pentru numere b,c):
sqrt((b^2+c^2)/2)>=1 care este echivalent cu a zice ca b^2+c^2>=2. Dar din ipoteza, b^2+c^2=a^2 (din teorema lui Pitagora). Si atunci, a^2>=2, echivalent cu a>=sqrt(2), ceea ce era de aratat.
Am notat cu a,b,c lungimile laturilor: BC, AC, respectiv AB.
Daca vrea cineva sa o scrie mai frumos… Nu fololsesc niciun program:D! Sper ca intelegi!
Da….! în 2 rânduri ….. bravo !
Care este cea mai mare valoare a produsului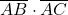
dacă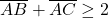 
?Mie îmi rezultă că 
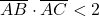.Greşesc cumva?
Suma a 2 vectori este un vector, dar tie iti apare ca un scalar(2)
Unde ai gasit exercitiul acesta?
In cerinta AB, AC si BC nu sunt vectori.