avem:
1+3+3^2+3^3+…+3^215
sa se demonstreze ca 2S+1 este cub perfect!
ne dam cu capatana de pereti de 3 zile si nu ne iese. probabil ne scapa o chestie simpla
pls, help?
neamieluuser (0)
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
avem:
1+3+3^2+3^3+…+3^215
sa se demonstreze ca 2S+1 este cub perfect!
ne dam cu capatana de pereti de 3 zile si nu ne iese. probabil ne scapa o chestie simpla
pls, help?
Inmultim cu 3 si obtinem
Acum scadem prima expresie din a doua, respectiv
adica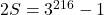
Cum 216 este divizibil cu 3, problema e aproape rezolvata …
E bine de retinut formula generala pentru sume de puteri
Formula se poate demonstra (daca nu o tinem minte) ca mai sus (conditia a diferit de 1).
aha, multumesc.
stiam ca tre’ sa fac ceva sa le aduc in forma sirului gauss, dar nu mi-a dat prin cap sa inmultesc cu 3.. am incercat tot soiul de alte artificii..😀
acum nedumerirea: sigur formula aia e de clasa a V-a? ca mie imi pare putin cam „sofisticata”…😈
Formula cu pricina nu stiu daca e in manualul de clasa a V-a, dar ideea e destul de simpla – inmultirea expresiei cu baza si apoi scaderea celor doua exprsii. In plus se mai da pe la concursuri, si o data invatata poate fi de folos.