Home/ Intrebari/Q 78648
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

gunty
maestru (V)
Pe: 2012-10-28T17:21:27+02:00 In: In:

Inegalitati – numere reale pozitive

1.
Fie a,b,c trei numere reale strict pozitive cu a+b+c=3. Sa se arate ca:

    \[ \frac{{a^2 }}{{bc(1 + \sqrt {bc} )}} + \frac{{b^2 }}{{ca(1 + \sqrt {ca} )}} + \frac{{c^2 }}{{ab(1 + \sqrt {ab} )}} \ge \frac{3}{2} \]

2.
Fie x,y,z numere reale strict pozitive cu proprietatea ca

    \[ x + y + z \ge \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \]

. Sa se arate ca:

    \[ \frac{{x + y + 1}}{{x + y + z^2 }} + \frac{{y + z + 1}}{{y + z + x^2 }} + \frac{{z + x + 1}}{{z + x + y^2 }} \le 3 \]

………………………………………………………………………………………………………………………………………………………………

*Stiu ca exista deja un subiect despre aceasta problema (problema 2), insa rezolvare tot nu e, si ma gandeam sa o readuc in discutie, poate are cineva o idee. Eu am reusit sa fac urmatoarea chestie:

    \[ \begin{array}{l} \frac{{x + y + 1}}{{x + y + z^2 }} + \frac{{y + z + 1}}{{y + z + x^2 }} + \frac{{z + x + 1}}{{z + x + y^2 }} \le 3 \\ \Leftrightarrow \frac{{x + y + 1}}{{x + y + z^2 }} - 1 + \frac{{y + z + 1}}{{y + z + x^2 }} - 1 + \frac{{z + x + 1}}{{z + x + y^2 }} - 1 \le 0 \\ \Leftrightarrow \frac{{1 - z^2 }}{{x + y + z^2 }} + \frac{{1 - x^2 }}{{y + z + x^2 }} + \frac{{1 - y^2 }}{{z + x + y^2 }} \le 0 \\ \end{array} \]

Si din relatia aia de la inceput se poate scoate ca x+y+z>=3. Sper sa va ajute macar putin.

Similare

5 raspunsuri

  1. ali
    maestru (V)

    Inegalitatea 1)
    \begin{array}{l} \sum {\frac{{{a^2}}}{{bc\left( {1 + \sqrt {bc} } \right)}}} \,\,\, \ge \limits_{{{\left( {MA - MG} \right)}_2}} \,\,\,\sum {\frac{{2{a^2}}}{{bc\left( {2 + b + c} \right)}}} \ge \frac{3}{4}\sum {\frac{{2{a^2}}}{{bc\left( {a + b + c} \right)}}} = \frac{1}{2}\sum {\frac{{{a^2}}}{{bc}}} \ge \frac{3}{2} \Leftrightarrow \sum {\frac{{{a^2}}}{{bc}}} \ge 3\\ {\left( {MA - MG} \right)_3}:\\ \sum {\frac{{{a^2}}}{{bc}}} \ge 3\sqrt[3]{{\frac{{{{\left( {abc} \right)}^2}}}{{bc \times ca \times ab}}}} = 3 \ge 3 \to {\rm{truth}}{\rm{.}} \end{array}
    Cred ca merge si cu CBS fortat … nu am încercat încă ….
    Ps: Am impresia ca atât inegalitatea 1 cât si 2 sunt probleme foarte cunoscute …(nu mai tin unde le-am văzut exact)

  2. ali
    maestru (V)

    Inegalitatea 2) care este mult mai simpla:
    \sum {\frac{{x + y + 1}}{{x + y + {z^2}}} \le } \sum {\frac{{x + y + 1}}{{x + y + z}} = \frac{{3 + 2\left( {x + y + z} \right)}}{{x + y + z}}} = \frac{3}{{x + y + z}} + 2 \le \frac{3}{3} + 2 = 3

  4. gunty
    maestru (V)

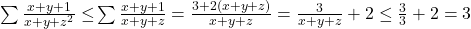
    M-am uitat peste rezolvari si problema e ca nu prea inteleg cum ai facut. De exemplu cum se arata, ca

        \[ \sum {\frac{{2a^2 }}{{bc\left( {2 + b + c} \right)}}} \ge \frac{3}{4}\sum {\frac{{2a^2 }}{{bc\left( {a + b + c} \right)}}} \]

    sau

        \[ \sum {\frac{{x + y + 1}}{{x + y + z^2 }}} \le \sum {\frac{{x + y + 1}}{{x + y + z}}} \]

    ? Multumesc!

  5. ghioknt
    profesor

    O idee: din ineg. mediilor deduc abc<=1 si atunci:

        \[ \begin{array}{l} \frac{{a^2 }}{{bc\left( {1 + \sqrt {bc} } \right)}} = \frac{{a^3 \sqrt a }}{{abc\left( {\sqrt a + \sqrt {abc} } \right)}} \ge \frac{{a^3 \sqrt a }}{{\sqrt a + 1}}. \\ Daca\,\,functia\,\,f\left( x \right) = \frac{{x^3 \sqrt x }}{{\sqrt x + 1}}\,\,este\,\,convexa\,\,(si\,\,eu\,\,cred\,\,ca\,\,este\,),\,\,atunci \\ \,f\left( a \right) + \,f\left( b \right) + \,f\left( c \right) \ge 3f\left( {\frac{{a + b + c}}{3}} \right) = 3 \cdot \frac{1}{2},\,\,ceeace\,\,demonstreaza\,\,prima\,\,inegalitate. \\ \end{array} \]

    Cu bine, ghioknt.

  6. gunty
    maestru (V)

    Frumoasa demonstratie, multumesc!

Raspunde

Raspunde