Home/ Intrebari/Q 78441
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Pollux
Pe: 2012-10-17T18:46:24+03:00 In: In:

Ecuatie exponentiala mai speciala

Sa se rezolve ecuatia stiind ca x apartine de [0;2pi]

2^sin(x)+2^cos(x)=3

Va multumesc!

Similare

9 raspunsuri

  1. ex-admin
    profesor

    Este evident ca ecuatia nu poate avea solutii in afara intervalului \[ \left[ {0;\frac{\pi }{2}} \right].

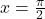    Este de asemenea evident ca x=0 si x=\frac{\pi }{2} sunt solutii. Probabil ca acestea sunt singurele solutii. Asta ramane de demonstrat!

  2. xor_NTG
    maestru (V)

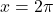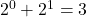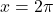    Daca luam x=2\pi se observa ca 2^0+2^1=3 deci x=2\pi este solutie.

  4. Pollux

    Cum a spus si admin,singurele solutii se afla in cadranul I,deoarece in celelalte cadrane ori sinusul ori cosinusul(ori ambele)este negativ.Deci,unul dintre termeni ar trebui sa fie subunitar.Deoarece sinusul si cosinusul se misca numai in intervalul [0;1] atunci celalalt ar putea(ideal)avea valoarea maxima 2.Adunat cu ceva subunitar ar da un numar evident mai mic decat 3=>Solutiile se afla numai in primul cadran.

    Am aflat de o inegalitate ce include si functia exponentiala si suna cam asa:

    2^n\>n^2+1,si sa zicem pentru orice n apartinand de (0;1)

    in inegalitatea asta inlocuind n cu sin(x)(care,dupa cum am spus,apartine de(0;1) ) se ajunge la

    2^sin(x)>sin^2 (x)+1(1)

    Analog se obtine si pentru cosinus(2)

    Adunand (1)si(2) se obtine ca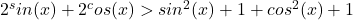 2^sin(x)+2^cos(x)>sin^2 (x)+1+cos^2 (x)+1 adica 2^sin(x)+2^cos(x)>3

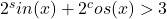
    Deci pentru orice numar din intervalul (0;1) nu s-ar putea atinge cazul de egalitate,cum se cere in cerinta.

    Daca am concluzionat mai sus ca sin si cos se misca numai in cadranul I,raman 2 numere de incercat(sau chiar 3):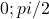0;pi/2(si 2pi)

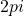    Si cum s-a aratat in mesajele trecute,acestea sunt solutii ale ecuatiei initiale.

    Nu stiu daca este o rezolvare corecta in totalitate,as vrea sa stiu daca am gresit undeva.Va multumesc!

  5. PhantomR
    expert (VI)
  6. ex-admin
    profesor

    Frumoasa rezolvare, Pollux chiar daca demonstrarea inegalitatii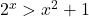 2^x > x^2 + 1 la nivel de clasa a X-a (fara derivate) nu vad cum s-ar putea face.

    Am o nedumerire: Ai reusit sa rezolvi problema dupa ce ai postat enuntul sau o stiai de la bun inceput?

  8. Pollux

    Demonstatia inegalitatii nu o stiu,am luat relatia ca atare.Intr-adevar nu aveam vreo idee despre cum s-ar putea rezolva,de aceea am si postat-o in acest forum.Odata gasita inegalitatea,rezolvarea a venit de la sine.

  9. Deny95

    Uitati o rezolvare a inegalitatii 2^x> x^2 +1 , oricare x real cu 0<x<1.
    Aplicand inegalitatea lui Bernoulli:

    (1+a)^n> 1+an, oricare ar fi a>-1 si n>0 avem:

    (1+1)^x> 1+x>1+x^2, pentru oricare x din intervalul (0,1).

    Scap vreun amanunt?

  10. xor_NTG
    maestru (V)

    Pare in regula.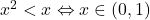 x^2<x \Leftrightarrow x \in (0,1) din cate stiu eu deci ar merge.

  12. PhantomR
    expert (VI)

Raspunde

Raspunde