1.Sa se descompuna in factori de gradul intai
a)![]()
![]()
![]()
2.Sa se determine valorile lui m astfel incat ecuatiile urmatoare sa aiba o radacina comuna.
![]()
![]()
3.Daca x si y satisfac relatia
![]()
Sa se determine ![]() cu y diferit de 0
cu y diferit de 0
4.Demonstrati ca Multimea![]()
Cu x si a reali.
5.Sa se arate ca multimea cu x real![]() are doua elemente oricare ar fi m real.
are doua elemente oricare ar fi m real.
6.Sa se determine m astfel incat multimea cu x real: ![]() sa aiba 3 elemente.Poate A avea doua elemente?
sa aiba 3 elemente.Poate A avea doua elemente?
Multumesc anticipat,Eduard.


1.a) Orice polinom de gradul II de forma se scrie
b) si c) Se procedeaza ca la punctul a).
2.a) Fie
3. Se imparte ecuatia cu
La ex 5 am calculat discriminantii:
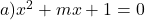

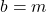
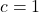
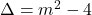
SI
Am gresit undeva?Daca nu,cum ar trebui sa continui?
Multumesc,Eduard🙂 .
Edit:Vreo idee despre exercitiile 4 si 6?
3. Ecuatia
4. Din
5. Calculand discriminantii celor doua ecuatii rezulta pentru ce valori ale lui
6. Presupun ca