Aflati nr. abcd care verifica egalitatea:
abcd + bcd+cd+d=3102
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Aflati nr. abcd care verifica egalitatea:
abcd + bcd+cd+d=3102
Relatia din enunt este echivalenta cu
1000*a+200*b+30*c+4*d=3102 de unde rezulta ca a<4.
Daca a=1 relatia din enunt este echivalenta cu
200*b+30*c+4*d=2102 .
Daca b<9 rezulta ca 200*b+30*c+4*d<_1600+34*9<2102 si deci in acest caz este obligatoriu ca b=9.
Ca urmare in acest caz avem ca b=9 si deci
30*c+4*d=302 si deci d trebuie sa dea restul 2 la impartirea cu 3 si 4*d sa se termine in 2, deci d=8 si ca urmare avem ca
30*c=270 si deci c=9 iar numarul cautat este 1998
Daca a=2 atunci
200*b+30*c+4*d=1102
de unde rezulta ca b=4 sau b=5 (a se vedea ordinul de marime)
Daca b=4 rezulta 30*c+4*d=302 cu d=8 si c=9 iar numarul cautat este
2498
Daca b=5 rezulta 30*c+4*d=102 cu b=0 contradictie
Din câte am văzut … ati obtinut doar 2 solutii 2498 si 1998 (am citi în graba sper ca nu am omis vre-unul) ….
😀
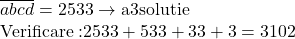
Solutia mea este asemănătoare rationamentului dvs cu o solutie în plus:
…….. vedeti dacă nu ati omis ceva