Am facut a) la b elementul neutru este -1 si stiu ca x*x’=x’*x=-1de aici nu mai stiu cum sa fac:|:|:|:|.daca poate cineva sa si explice ar fi excelent.Va multumesc
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Deci avem cerintele: b) elementele simetrizabile:
b) elementele simetrizabile:
avem o lege de compozitie
1. observam ca legea nu poate fi descompusa, o lasam asa
2. pentru a afla elementele simetrizabile avem nevoie de elemntul neutru.
a. element neutru: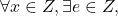 a.i.
a.i.



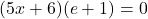

Axioma:
si :
Am aflat elementul neutru.Acum pe cel simetrizabil
b. elemntul simetrizabil
 a.i.
a.i.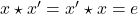




Axioma:
5x+6=-1 rezulta o slutie
Solutie finala x’=-1
c.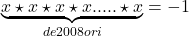 stim ca elemntul neutru se conformeaza la
stim ca elemntul neutru se conformeaza la  si ca elemntul simetrizabil este x’=-1.Deci inmultim ecuatia cu un x’ si avem
si ca elemntul simetrizabil este x’=-1.Deci inmultim ecuatia cu un x’ si avem 
 trecem minusul in dreapta si procedeul se repeta de 2008 ori si ajungem la solutie x=-1
trecem minusul in dreapta si procedeul se repeta de 2008 ori si ajungem la solutie x=-1
Legea de compozitie data se poate scrie si ;x*y=[(5.x+6).(5.y+6)-6]/5.
Elementul neutru „e” va fi dat de relatia ; x*e=e*x=[(5.x+6).(5.e+6)-6]/5=x -> e=-1 -elemantele multimii pe care se aplica legea sunt in Z.
Elementul simetrizabil al lui „x” -in caz general , il vom nota cu „x’ ” si trebue, conf . definitiei , sa avem;x*x’=x’*x=e sau; [(5.x+6).(5.x’+6)-6]/5=e=-1 -> 5.x’+6=1/(5.x+6), sau x’=[(1/(5.x+6)) – 6]/5 .Ca x’ sa fi in Z trebue ca x=-1 si este singurul element ca x’ sa fie in Z. Valoarea lui x’ este ; x’=-1 si normal , elementul simetrizabil al lui x’ va fi ; (x’)’=x=-1
c]. Avand in vedere ca x’=x=e=-1 si ca x*x’=e=x ,pentru x=-1, vom putea scrie ca ; x’*x=x*x=x=x’=-1 -> Deci , numai pentru x=-1 vom avea; x*x*…de n ori =(x*x)*(x*x)*…*(x*x)=x*x*x*…de n/2 ori= s.a.m.d=x=-1