Am urmatorul exercitiu:
![Rendered by QuickLaTeX.com \[ E\left( x \right) = \sqrt {\log _a \sqrt[4]{{ax}} + \log _x \sqrt[4]{{ax}}} + \sqrt {\log _a \sqrt[4]{{\frac{x}{a}}} + \log _x \sqrt[4]{{\frac{a}{x}}}} = a \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ee4f09177389c4587246e6390b4ce1ee_l3.png)
Se pune problema exprimarii lui x in functie de a.
Am aplicat proprietatile logarimtului si ale radicalului astfel:
![Rendered by QuickLaTeX.com \[ \begin{array}{l} E\left( x \right) = \sqrt {\log _a \sqrt[4]{{ax}} + \log _x \sqrt[4]{{ax}}} + \sqrt {\log _a \sqrt[4]{{\frac{x}{a}}} + \log _x \sqrt[4]{{\frac{a}{x}}}} = a,\,x \in \left( {1,\infty } \right) \\ E\left( x \right) = \sqrt {\frac{1}{4}\log _a \left( {ax} \right) + \frac{1}{4}\log _x \left( {ax} \right)} + \sqrt {\frac{1}{4}\log _a \left( {\frac{x}{a}} \right) + \frac{1}{4}\log _x \left( {\frac{a}{x}} \right)} = a \\ E\left( x \right) = \sqrt {\frac{{\log _a a + \log _a x + \log _x a + \log _x x}}{4}} + \sqrt {\frac{{\log _a x - \log _a a + \log _x a - \log _x x}}{4}} = a \\ E\left( x \right) = \sqrt {\frac{{\log _a x + \frac{1}{{\log _a x}} + 2}}{4}} + \sqrt {\frac{{\log _a x + \frac{1}{{\log _a x}} - 2}}{4}} = a \\ \log _a x = y \Rightarrow E\left( x \right) = \sqrt {\frac{{y^2 + 2y + 1}}{{4y}}} + \sqrt {\frac{{y^2 - 2y + 1}}{{4y}}} \Rightarrow \sqrt {\frac{{\left( {y + 1} \right)^2 }}{{4y}}} + \sqrt {\frac{{\left( {y - 1} \right)^2 }}{{4y}}} = a \\ \Rightarrow E\left( x \right) = \frac{{\left| {y + 1} \right|}}{{2\sqrt y }} + \frac{{\left| {y - 1} \right|}}{{2\sqrt y }} = a \Rightarrow \frac{{\left| {y + 1} \right| + \left| {y - 1} \right|}}{{2\sqrt y }} = a \Rightarrow \left| {y + 1} \right| + \left| {y - 1} \right| = 2a\sqrt y \Rightarrow \\ \Rightarrow E\left( x \right) = \left| {\log _a x + 1} \right| + \left| {\log _a x - 1} \right| = 2a\sqrt {\log _a x} \\ \\ \end{array} \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-0a2777614b13587dc6902ef88da3250b_l3.png)
Am verificat calculul de cateva ori, deci nu cred ca ar putea fi ceva gresit. M-am blocat aici pentru ca nu stiu cum sa explicitez modulele. Ma incurca acei logaritmi. Am incercat sa iau pe cazuri adica a sa fie in (0,1) dar nu ajung nicaieri.
Multumesc.


Din conditiile de existenta ale logaritmilor avem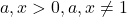 . Deci
. Deci 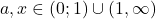 , pentru care avem
, pentru care avem 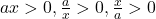 , adica sunt verificate si conditiile de existenta ale radicalilor.
, adica sunt verificate si conditiile de existenta ale radicalilor.
Sa ne jucam cu conditiile de existenta😀 . Pentru ca cele doua fractii sa existe avem 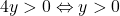 . Deoarece
. Deoarece 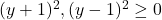 , pentru ca cei doi radicali sa existe trebuie sa avem
, pentru ca cei doi radicali sa existe trebuie sa avem 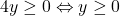 . Asadar
. Asadar 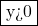 .
. 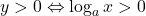 si cum
si cum 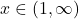 (caci asa parca scrie la inceput), acest lucru este echivalent cu
(caci asa parca scrie la inceput), acest lucru este echivalent cu 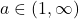 .
.
Sa avem in vedere faptul ca
Dupa cum ati scris, vom avea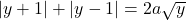 . Distingem doua cazuri:
. Distingem doua cazuri:
1.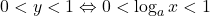 . Cum avem deja
. Cum avem deja 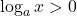 , mai ramane doar ca
, mai ramane doar ca 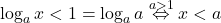 . In acest caz avem
. In acest caz avem 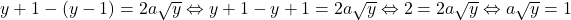 . Ambii membri fiind pozitivi, ridicam relatia la patrat spre a obtine cea echivalenta
. Ambii membri fiind pozitivi, ridicam relatia la patrat spre a obtine cea echivalenta 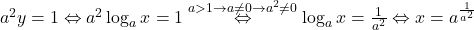 . Cum
. Cum 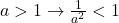 , avem
, avem 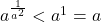 (conditia cazului). Mai avem de verificat
(conditia cazului). Mai avem de verificat 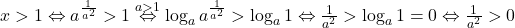 , adevarat si deci valoarea gasita pentru
, adevarat si deci valoarea gasita pentru  este intr-adevar solutie.
este intr-adevar solutie.
2.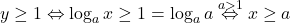 . Avem
. Avem 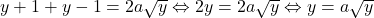 . Cum
. Cum 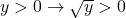 , impartim prin
, impartim prin  spre a obtine
spre a obtine 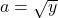 . Cum ambii membri sunt pozitiv, ridicam la patrat si obtinem echivalent
. Cum ambii membri sunt pozitiv, ridicam la patrat si obtinem echivalent 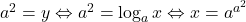 . Cum
. Cum 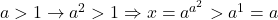 (conditia cazului) , iar cum
(conditia cazului) , iar cum  avem
avem 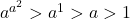 , deci aceasta valoare este si ea o solutie.
, deci aceasta valoare este si ea o solutie.
In final avem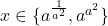 cu
cu  .
.
Multumesc mult PhantomR!
Cu multa placere!:D Sper sa fie bine.
E perfect, raspunsurile coincid cu cele de la sfarsitul cartii. Va multumesc pentru ca m-ati facut sa inteleg ideea.
Ma bucur ca v-am fost de ajutor!🙂 Cu multa placere inca o data!