Sa se studieze injectivitatea, bijectivitatea si surjectivitatea functiilor:
a) f:R->R, f(x)={x^2 + radical din 2x, x apartine Q
{x, x apartine R/Q
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
O intrebare: Sper ca am interpretat corect ramura de sus a functiei. M-am gandit ca nu ar putea fi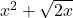 , deoarece aceasta expresie este definita doar pentru
, deoarece aceasta expresie este definita doar pentru  .
.
Fie functiile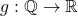 definita prin
definita prin 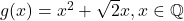 si
si 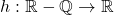 definita prin
definita prin 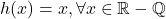 .
.
Pentru ca sa fie injectiva trebuie sa avem
sa fie injectiva trebuie sa avem  injective si
injective si 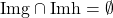 . Pentru ca
. Pentru ca  sa fie surjectiva trebuie sa avem
sa fie surjectiva trebuie sa avem 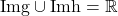 . In plus, avem
. In plus, avem  bijectiva
bijectiva 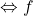 injectiva si surjectiva.
injectiva si surjectiva.
Pentru
Deoarece
Rezulta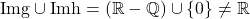 si deci
si deci  este nesurjectiva.
este nesurjectiva.
 BIJECTIVITATE
BIJECTIVITATE nu este nici injectiva si nici surjectiva, rezulta
nu este nici injectiva si nici surjectiva, rezulta  nu este bijectiva.
nu este bijectiva.
Cum