Ma puteti ajuta cu urmatorul exercitu?
Sa se arate ca are loc egalitatea x,(y)+y,(z)+z,(x)=x,y(x)+y,z(x)+z,x(y), unde x, y si z sunt cifre.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Cred ca ati facut o greseala de redactare la membrul drept, adica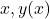 , unde eu am luat ca fiind
, unde eu am luat ca fiind 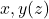 .
.
Asadar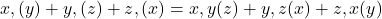
Adunam numerele din primul membru astfel:
x,yyyyy….+
y,zzzzz….
z,xxxxx…..
(x+y+z),(x+y+z)(x+y+z)……
Adunam numerele din al doilea membru astfel:
x,yzzzz….+
y,zxxxx….
z,xyyyy…..
(x+y+z),(x+y+z)(x+y+z)……
Deci egalitatea este adevarata.
x+y+z poate sa depaseasca 10 caz in care se aduna transport. Rezolvarea lui PhantomR e mai sigura (no offence).
Un exemplu de scriere a unui numar:
Da domle sunt de acord cu tine n-am zis ca rezolvarea matale e proasta doar ca e fortata un pic nota cu acel 13 din exemplul tau cifra.