Sa se arate ca daca a,b,c apartin (1,+infinit), atunci:
log din baza a din [(a+b+c)/3] + log din baza b din [(a+b+c)/3]+ log din baza c din [(a+b+c)/3] >=3.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Deoarece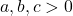 , din inegalitatea dintre media aritmetica si cea geometrica avem
, din inegalitatea dintre media aritmetica si cea geometrica avem ![Rendered by QuickLaTeX.com \frac{a+b+c}{3}\geq \sqrt[3]{abc}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-e33a274853555753b23e7727ae088ece_l3.png) . Atunci, cum
. Atunci, cum 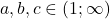 avem
avem ![Rendered by QuickLaTeX.com \sum \log_a \frac{a+b+c}{3}\geq \sum \log_a \sqrt[3]{abc}=\sum \frac{1}{3}\log_a(abc)=\frac{1}{3}\sum \log_a (abc)](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ade778e1b9596a80dca4f40f95166877_l3.png) . Incercam sa demonstram ca
. Incercam sa demonstram ca 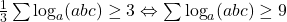 , adica
, adica 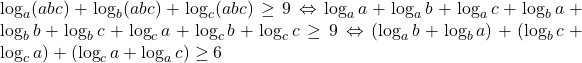 (*).
(*).
Deoarece sunt de aceeasi parte a lui
sunt de aceeasi parte a lui  , toti logaritmii din membrul stang al inegalitatii anterioare sunt strict pozitivi. Aplicand inegalitatea dintre media aritmetica si cea geometrica avem
, toti logaritmii din membrul stang al inegalitatii anterioare sunt strict pozitivi. Aplicand inegalitatea dintre media aritmetica si cea geometrica avem 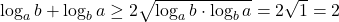 si insumand aceasta inegalitate cu celalalte doua analoage rezulta inegalitatea (*).
si insumand aceasta inegalitate cu celalalte doua analoage rezulta inegalitatea (*).
EGALITATE: Egalitatea se atinge daca in cele doua dati incare am aplicat inegalitatea mediilor avem egalitati. Conditia de egalitate in prima inegalitate aplicata este , iar in a doua (care de fapt contine trei aplicatii)
, iar in a doua (care de fapt contine trei aplicatii) 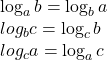 , ambele echivalente cu
, ambele echivalente cu  .
.