sti cineva cum se face exercitiul
daca x+y+z=2kπ, , sa se arte ca sinx+siny+sinz=(-1)**k+1*4sinx/2*siny/2*sinz/2
trbuie exprimate x, y sau z in fct de x+y+z=2kπ
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
putem face sinx+siny+sinz+sin0 si sa grupam ,iar duma il fom exprima pe z in fct de x , y si 2kπ
Ajutatima va rog!
Daca M este un punct oarecare pe cercul circumscris unui triunghi echilateral ABC ,aratati ca expresia MA(la a doua)+MB(la a doua)+MC(la a doua) nu depinde de pozitia lui M.
Cu relatia lui Leibniz (Demonstratie aici: http://www.scribd.com/doc/50103673/mate) avem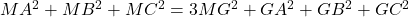 , unde notatiile sunt cele uzuale.
, unde notatiile sunt cele uzuale.
Cum este pe cercul circumscris si deoarece triunghiul este echilateral avem
este pe cercul circumscris si deoarece triunghiul este echilateral avem 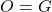 , rezulta
, rezulta 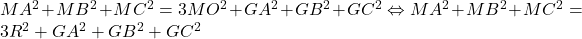 , adica expresia data nu depinde de pozitia punctului
, adica expresia data nu depinde de pozitia punctului  .
.
Stabiliti natura triunghiului ABC in care a+b=2c si sinA+sinB= radical din 3[/code]
Se considera un triunghi ABC in care b(la a doua)+c(la a doua)+bc=a(la a doua).Determinati masura unghiului A si aratati ca: ctgB*ctgC=>(mai mare sau egal)3.*=inmultire
VA ROG SA FACETI CATE UN TOPIC (SUBIECT) SEPARAT PENTRU FIECARE PROBLEMA!
Sa aplicam teorema sinusurilor si sa tinem seama de relatiile impuse de problema, deci ;
a+b=2c -> 2.R.(sinA+sinB)=2.2R.sinC , sau ; sinC=(radical din 3)/2-> 1]. (<C)’=60gr. sau ; 2]. (<C)”=120gr.
Dar sinA+sinB=2sin[(A+B)/2] . cos[(A-B)/2]=(radical din 3) , sau ;1]. sin(90-C’/2).cos[(A-B)/2]=(radical din 3)/2, sau ;cos(C’/2).cos[(A-B)/2]=cos(30).cos[(A-B)/2]=[(radical din 3)/2].cos[(A-B)/2]=(radical din 3)/2 ->
cos[(A-B)/2]=1->A=B . Cum C’=60gr si A=B si 60+A+B=60+2.A=180->A=B=C=60gr ->echilateral.
Cazul 2]. Plecam de la ;cos(C”/2).cos[(A-B)/2]=cos(60).cos[(A-B)/2]=(radical din 3)/2 -> (1/2).cos[(A-B)/2]=(radical din 3)/2 ->cos[(A-B)/2]=
(radical din 3)>1 solutie neverosimil
Avem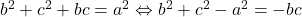 . Dar din teorema cosinusului avem
. Dar din teorema cosinusului avem 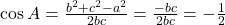 . Cum
. Cum 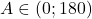 rezulta
rezulta 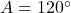 .
.
Inegalitatea sigur e buna🙂 ?
Pentru domnul „Asasin”. Aplicand teorema generala a lui Pitagora , rezulta cosA=-1/2, sau ; <A=120gr. Din ; ctgB.ctgC>=3 ->cosB.cosC>= 3.sinB.sinC, sau ; cosB.cosC-sinB.sinC>=2sinB.sinC, sau ;cos(B+C)>=
cos(B-C)-cos(B+C) , sau ; 2.(-cosA)=-2.(-1/2)=1=cos(B-C) sau B=C=30gr Deci triunghiul este isoscel cu ; <A=120 si B=C=30gr
da e buna phantom
Domnule DD, cred ca trebuia sa demonstrati acea inegalitate nu sa o folositi🙂 .
Domnule TheAssassin11, multumesc pentru raspuns!:)
daca ai putea face si asta domnule phantom ctgB*ctgC=>(mai mare sau egal)3. este tot de la acea problema va rog frumos.multumesc
Din pacate nu sunt sigur cum as putea rezolva acea inegalitate cu cotangente.
Eu unul nu mai inteleg nimic… ce se cere… omul asta a pus cred >5 probleme aici… doar azi! PhantomR daca stii cumva problema posteaz-o te rog in latex! Multumesc.
Ok. Cred ca ma apuc de ea maine… de-abia i-am facut prb cu AI=4*R*sin(B/2)*sin(C/2) pe care o s-o postez tot maine! Multzam!