Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Este o problema din Culegerea De Evaluare Nationala testul 26 partea a II-a ex.5 pag.136
Aratati ca nr 3 * a la patrat + 4 rad 3*a+9 este pozitiv,oricare ar fi a 5 apartine la R.
Multumesc anticipat!
Expresia se poate scrie ca 3a^2 + 4*radical de 3*a + 4 +5.
Se observa ca primii trei termeni alcatuiesc un binom la patrat:
(Radical de 3*a + 3)^2,iar restul de 5 ramane asa cum e.
In final,expresia se poate scrie ca
(Radical de 3*a + 3)^2 + 5.Primul termen este pozitiv deoarece este un patrat iar al doilea(adica 5) este categoric pozitiv.O suma de numere pozitive nu poate da altceva decat un numar pozitiv.
Nota:x^2=x la patrat
Multumesc :*
Nu inteleg enuntul………🙄 Scrie te rog mai clar sau cu „Tex” („LaTex”)….Daca ai vrut sa scrii cumva 
atunci E=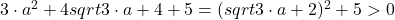
pentru orice numar real 
.Ce inseamna ca un numar este pozitiv?Numarul zero este un numar pozitiv?