Home/ Intrebari/Q 77050
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Laur
Pe: 2012-05-31T15:04:00+03:00 In: In:

Functie

Fie f : (0,infinit)->(0,infinit), f(x)=x+1/x
Demonstrati ca f este strict monotona pe fiecare din intervalele (0,1) si [1,infinit].

Similare

8 raspunsuri

  1. PhantomR
    expert (VI)

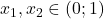    1) f strict monotona pe (0;1). Fie x_1,x_2\in (0;1) astfel incat x_1<x_2. Avem f(x_1)-f(x_2)=(x_1-x_2)+\left( \frac{1}{x_1}-\frac{1}{x_2} \right)=x_1-x_2+\frac{x_2-x_1}{x_1x_2}=x_1-x_2-\frac{x_1-x_2}{x_1x_2}=(x_1-x_2)\left( 1-\frac{1}{x_1x_2}\right)=(x_1-x_2)\cdot \frac{x_1x_2-1}{x_1x_2}.

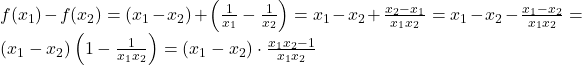    Deoarece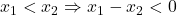 x_1<x_2 \Rightarrow x_1-x_2<0 (1). Deoarece 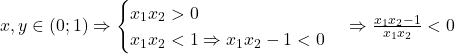x,y\in(0;1) \Rightarrow \begin{cases} x_1x_2>0 \\ x_1x_2<1 \Rightarrow x_1x_2-1<0 \end{cases} \Rightarrow \frac{x_1x_2-1}{x_1x_2}<0 (2). Din relatiile (1),(2) deducem 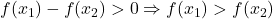f(x_1)-f(x_2)>0 \Rightarrow f(x_1)>f(x_2), adica functia este strict descrescatoare pe (0;1).

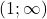    2) f strict monotona pe (1;\infty). Va descurcati dumneavoastra sa faceti acest caz pe baza modelului de la cazul 1)?:)

  2. Laur

    D-abia am ajuns la aceasta lectie..nu cred ca reusesc

  4. PhantomR
    expert (VI)

    O mentiune: faptul ca am scris „1) f strict monotona pe (0;1)” este ceea ce urmeaza a fi demonstrat.

    Ce este o functie strict monotona?

  5. doctal

    \it{f(1)=1+1=2\\\;\\f(2)=2+\frac{1}{2}=\frac{5}{2} >2\\\;\\f(3)=3+\frac{1}{3} = \frac{10}{3} > \frac{5}{2} >2\\\;\\Deci, f(3)>f(2)>f(1)\\\;\\Aceasta ultima relatie ne ofera impresia unei cresteri a functiei. \\\;\\Intuim ca functia ar putea fi strict crescatoare pe intervalul [1, \infty)\\\;\\Este necesara o demonstratie a acestui fapt.\\\;\\Fie a, b \in [1, \infty), a>b.\\\;\\Vom arata ca f(a)>f(b) .\\\;\\f(a) = a+\frac{1}{a} = \frac{a^2 + 1}{a} ; f(b) = b+\frac{1}{b} = \frac{b^2 + 1}{b }\\\;\\f(a) > f(b) \Leftrightarrow \frac{a^2 + 1}{a} > \frac{b^2 + 1}{b} \Leftrightarrow a^2b+b > ab^2+a \Leftrightarrow a^2b - ab^2 > a - b\Leftrightarrow\\\;\\\Leftrightarrow ab(a - b) > a - b |_{ : (a - b)} \Leftrightarrow ab > 1 (A).\\\;\\Deci, f(x) este strict crescatoare pe intervalul [1, \infty).}

  6. sandy_sc
    maestru (V)

    Fie 1<X1<X2
    f(X1)=X1+1/X1
    f(X2)=X2+1/X2
    f(X1)-f(X2)=(X1_X2)+1/X1-1/X2=calcule=(x1-X2)+[-(X1_X2)/X1*X2]<0 deoarece prima paranteza e clar <0., iar a 2 paranteza desi e pozitiva e mai mica in valoare absoluta decat prima dincauza numaratorului supra unitar
    f descrescatoare
    Erata numitor in loc de numarator

  8. edy8
    maestru (V)

    sandy_sc wrote: Fie 1<X1<X2
    f(X1)=X1+1/X1
    f(X2)=X2+1/X2
    f(X1)-f(X2)=(X1_X2)+1/X1-1/X2=calcule=(x1-X2)+[-(X1_X2)/X1*X2]<0 deoarece prima paranteza e clar <0., iar a 2 paranteza desi e pozitiva e mai mica in valoare absoluta decat prima dincauza numaratorului supra unitar
    f descrescatoare

    ?!

  9. Laur

    Va multumesc mult pentru ajutor! 😀

  10. PhantomR
    expert (VI)

    Cu multa placere!:)

Raspunde

Raspunde