„Sa se rezolve ecuatia in x:
![]()
” Eu am rezolvat exercitiul in sensul ca am explicitat fiecare modul:
![Rendered by QuickLaTeX.com \[ \begin{array}{l} \left| {x + 1} \right| = \left\{ \begin{array}{l} x + 1 \Leftrightarrow x + 1 \ge 0,x \ge - 1; \\ - x - 1 \Leftrightarrow x + 1 < 0,x < - 1; \\ \end{array} \right. \\ \left| {x - 1} \right| = \left\{ \begin{array}{l} x - 1 \Leftrightarrow x - 1 \ge 0,x \ge 1; \\ - x + 1 \Leftrightarrow x - 1 < 0,x < 1; \\ \end{array} \right. \\ \left| {x - 3} \right| = \left\{ \begin{array}{l} x - 3 \Leftrightarrow x - 3 \ge 0,x \ge 3; \\ - x + 3 \Leftrightarrow x - 3 < 0,x < 3; \\ \end{array} \right. \\ \end{array} \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-c827c6f4bcaea886aa290bdfefc8eba2_l3.png)
si apoi am luat pe cazuri. De ex primul caz cand
![]()
de unde l-am scos pe x, apoi am trecut la urmatorul caz si asa mai departe numai ca, la sfarsit mi-au iesit o gramada de valori si intervale ale lui x de la diferite cazuri si nu stiu ce sa fac cu ele, sa le intersectez sau sa le reunesc. In orice caz, oricum nu cred ca e bine cum am facut eu si as dori un sfat, o sugestie ceva.


Scrie acum ec. fara module pe intervalele ; a]. (-infinit , -1) rezolva ec si ia ca bune solutiile ce apartin acestui interval . b]. [-1 , 1), scrie ec , rezolv-o si ia ca bune numai solutiile ce apartin acestui interval. c], [1 , 3), idem , ca la a]. si b]. d]. [3 , infinit) idem. Lucreaza incet si atent . Nu te grabi. Succes
Puteti folosi si inegalitatea modulului:
Am aplicat inegalitatea modulului de doua ori. Pentru ca in primul caz sa avem egalitate trebuie ca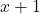 si
si  sa aiba acelasi semn
sa aiba acelasi semn 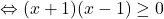 , de unde
, de unde 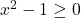 . Daca luam membrul stang ca o functie de gradul doi, atunci obtinem ca solutiile sale sunt
. Daca luam membrul stang ca o functie de gradul doi, atunci obtinem ca solutiile sale sunt 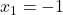 si
si 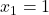 , ceea ce implica
, ceea ce implica ![Rendered by QuickLaTeX.com x\in (-\infty,-1] \cup [1,\infty)](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-6e523869b2cdbd51ea574edc1505bdbe_l3.png) .
.
In al doilea caz avem egalitate daca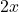 si
si 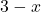 au acelasi semn
au acelasi semn 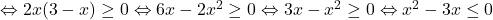 . Membrul stang luat ca o functie de gradul doi are radacinile
. Membrul stang luat ca o functie de gradul doi are radacinile 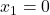 si
si 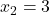 , de unde
, de unde ![Rendered by QuickLaTeX.com x\in[0,3]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-cc6426b2da5d7617cb9f289b23515110_l3.png) .
.
Atunci avem![Rendered by QuickLaTeX.com x\in[-3,\infty) \cap ((-\infty,-1]\cup [1,\infty)) \cap [0,3]=[1,3]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-5e5f0fc185c6f5596ca67d62b46882ce_l3.png) .
.
Mai sunt curios de-o chestie. De ce rezolvarea mea nu e corecta? Care e greseala de rationament?
Daca am inteles bine ce ati incercat sa faceti, eu nu vad nicio greseala, doar ca banuiesc ca e destul de complicat sa „alegeti” acele cazuri🙂 .
V-am raspuns la „MP”.🙂
Ca sa-ti raspund, mi-ar trebui problema. Am uitat-o . Daca o reeditezi , fa-ma atent, cumva.
A aparut problema .Deci;
In intervalul ;(-infinit , -1), avem ec; -x-1-x+1-x+3=x+3 , sau 4.x=0->x=0
, dar zero nu apartine intervalului si nu poate fi solutie.
In intervalul ; [-1 , 1), avem ec; x+1-x+1-x+3=x+3 , sau ; 2.x=1->x=1 , nu apartine intervalului si nu este solutie.
In intervalul ; [1 , 3) , avem ec. x+1+x-1-x+3=x+3 , sau ;x+3=x+3 identitate si x poate lua orice valoare din interval . In acest caz , toate punctele intervalului sunt solutii, adica toate elementele itervalului ; [1 , 3)
sunt solutii .
In intervalul; [3 , infinit) , avem ec.; x+1+x-1+x-3=x+3 , sau 2.x=6->x=3 , apartine intervalului si este solutie.Reuni solutiile din ultimile 2 cazuri si avem ; [1 , 3)U{3}=[1 , 3]. Elementele acestui interval inchis , sunt solutiile cautate.
Am cautat a fi cat mai clar.Cu respect.DD