Mă poate ajuta cineva : Verificați dacă următoarele șiruri sunt monotone, mărginite și aflați limita lor .
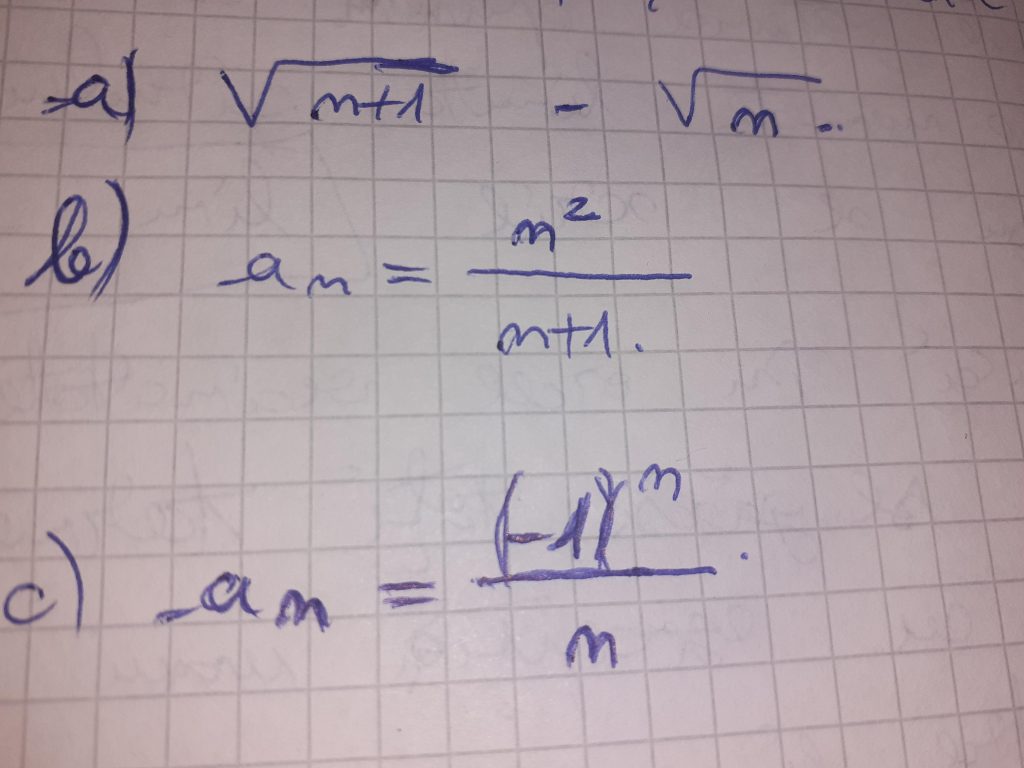
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Am stiut doar monotonia sa o rezolv! Sper ca te ajuta!


a)Rationalizam:
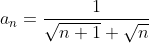
Monotonia
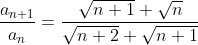
Calculam raportul
Se observa usor ca acest raport este <1, ceea ce inseamna ca sirul nostru este monoton, anume strict descrescator.
Marginirea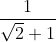 .
.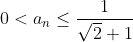
Sirul fiind descrescator, este marginit la dreapta de primul sau termen, care este
Pentru marginirea la stanga, observam ca sirul este pozitiv.
Deci
Limita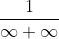 , adica 0.
, adica 0.
Limita la infinit este de forma
b)Rescriem ca:
}{n+1}-\frac{2n+2-1}{n+1}=n+1-\frac{2n+2}{n+1}+\frac{1}{n+1}=n+1-2+\frac{1}{n+1}=n-1+\frac{1}{n+1})
Monotonie(n+2)}-\frac{n+2}{(n+1)(n+2)}=1-\frac{1}{(n+1)(n+2)})
Calculam
Se observa imediat ca aceasta diferenta este pozitiva, deci sirul nostru este crescator.
Marginire
Revenim la forma din enunt. Sirul fiind crescator, marginirea la stanga este primul termen al acestuia, adica 0. La dreapta in schimb, sirul nu are margine, limita sa la infinit fiind infinit.
Limita
Limita obisnuita de raport de polinoame, adica infinit.
c)Sirul nu exista in 0. Ignorand acest lucru:
Monotonie
Primii 3 termeni ai sirului sunt -1, 1/2, respectiv -1/3, desi sirul nu este monoton.
Marginire
Luand sirul format cu indicii pari ai celui dat, observam ca limita sa la 0 este infinit. Sirul initial nu poate fi marginit, considerand faptul ca unul dintre subsirurile sale nu este.
Limita
Limita este de forma 1/inf sau -1/inf, deci 0.
Te rog ma poti ajuta la întrebarea de azi
Multumesc . Mă puteți ajuta la un alt exercitiu? E foarte urgent