Demonstrati: (a+b+c)(1/a+1/b+1/c) >9 , a, b, c reale >0
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sa facem inmultirea si vom avea ; 3+(a/b+b/a)+(b/c+c/b)+(c/a+a/c)>=
3+2+2+2=9. Mult prea simplu.
Scrisesem asa dar nu m-am gandit sa-i grupez😳 Inca o intrebare. Pot arata ca este strict mai mare decat 9? Pentru ca inegalitatea face parte dintr-un exercitiu cu functie in care imi cere ca graficul functiei sa nu taie Ox. Pun conditia ca ∆<0, iar ∆= 36-4(a+b+c)(1/a+1/b+1/c), asa ca mi-ar trebui ca parantezele sa fie strict mai mare ca 9
Dar va multumesc ca mi-ati raspuns
In egalitatile de tipul
, unde 
exista egalitate daca si numai daca 
(deoarece inegalitatea este echivalenta, prin aducere la acelasi numitor, cu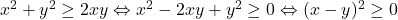 
, adevarat si cu egalitate daca si numai daca 
).
Atunci in inegalitatea data exista egalitate, apeland la solutia domnului DD, pentru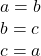
[tex]\Leftrightarrow a=b=c[/tex]. Probabil ca in problema se specifica ca cele trei numere sunt distincte si atunci inegalitatea este stricta 🙂 .