1. Fie A o multime nevida.Sa se arate ca multimea A este finita daca si numai daca are loc una din proprietatile:
a). orice functie injectiva f:A->A este si functie surfectiva
b). orice functie surjectiva f:A->A este si functie injenctiva
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Si in cazul a]. si in cazul b]. functia ; f ; A -> A , este bijectiva. In acest caz, fiecarui element din domeniu ii corespunde un anumit element din codomeniu si numai un element. Deci, numarul elementelor din domeniu este egal cu numarul elementelor din codomeniu, din care cauza multimea A poate fi oricat de mare, dar nu infinita. (nu se poate analiza proprietatea de bijectivitate , la infinit). (parerea mea).
Eu cred ca se poate🙂 . De exemplu,  este bijectie
este bijectie 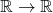 .
.
Deci,cum e pana la urma.Si daca se poate sa mi-o explicati ca o sa am in genu la asta maine la test.Va rog
Sunteti in clasa de elita? Faceti asa ceva la clasa :O?
Daca A este finita atunci fie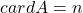 si fie
si fie 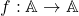 o functie oarecare.
o functie oarecare.
a) Daca este injectie atunci sa presupunem ca ar exista
este injectie atunci sa presupunem ca ar exista 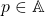 astfel incat
astfel incat 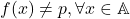 . Deoarece din injectivitate
. Deoarece din injectivitate 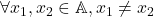 avem
avem 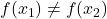 rezulta ca functia ia cel putin
rezulta ca functia ia cel putin  valori diferite. Atunci presupunerea facuta ar implica faptul ca
valori diferite. Atunci presupunerea facuta ar implica faptul ca  are cel putin
are cel putin  elemente, contradictie cu faptul ca numarul de elemente al multimii
elemente, contradictie cu faptul ca numarul de elemente al multimii  este exact
este exact  . Deci nu avem niciun element
. Deci nu avem niciun element 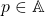 astfel incat
astfel incat 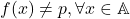 , de unde
, de unde  surjectie.
surjectie.
b) Daca este surjectie atunci
este surjectie atunci  ia toate valorile din
ia toate valorile din  . Sa presupunem ca exista
. Sa presupunem ca exista 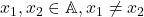 astfel incat
astfel incat  . Atunci in multimea
. Atunci in multimea  exista cel mult
exista cel mult  elemente cu imagini distincte prin functia
elemente cu imagini distincte prin functia  , contradictie cu faptul ca functia ia exact
, contradictie cu faptul ca functia ia exact  valori distincte, din surjectivitate. Asadar
valori distincte, din surjectivitate. Asadar 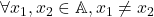 avem
avem 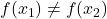 , ceea ce atrage injectivitatea functiei.
, ceea ce atrage injectivitatea functiei.
NOTA: Sper ca este cat de cat inteligibila si corecta solutia. O sa ma mai gandesc eventual si la implicatia reciproca.
P.S Mult succes maine la test!!!
EDIT: O alta solutie pentru implicatia directa (probabil veti intelege mai bine) se poate gasi la paginile 35-36 de la http://www.scribd.com/doc/33307796/Lectii-de-Algebra .
Multumesc din toata inima,mi-ai fost de mare ajutor!:*
Cu multa placere! Sper ca v-ati descurcat la test!
Am postat problema si pe un alt forum. Aici este demonstrata echivalenta celor trei relatii (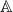 finita si cele doua proprietati 1) si 2)).
finita si cele doua proprietati 1) si 2)).
Va multumesc si eu ca ati postat problema, este simpatica!:)
N-ai pentru ce,eu iti multumesc mai mult! Daca ai putea sa ma ajuti si la celelalte probleme la matematici financiare,ar fi super! Mersi inca o data!
Cu cea mai mare placere! La matematici financiare nu cred ca ma prea descurc.. Cu multa placere!
Am uitat cred sa las link-ul catre acea rezolvare: