Consideram numerele a=2+radical de 3 si b=2-radical de 3 .Pentru fiecare n apartine de N notam x indice n=a^n+b^n.
a)Demonstrati ca x indice (n+2) – 4x indice (n+1) + x indice n = 0,pentru orice numar natural n.
b)Demonstrati ca (2 + radical de 3 )la puterea n + (2- radical de 3 )la puterea n este un numar par,pentru orice numar natural n.
c)Aratati ca partea intreaga a numarului real ala puterea n este impara,oricare ar fi n natural.


a)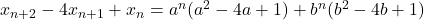 .
.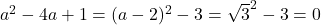 si
si 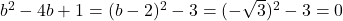 , de unde rezulta concluzia.
, de unde rezulta concluzia.
Dar
b) Avem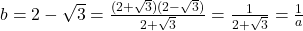 . Atunci
. Atunci 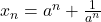 . Vom demonstra prin inductie matematica faptul ca
. Vom demonstra prin inductie matematica faptul ca  este par.
este par.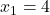 ,
, 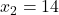 -> ambele pare.
-> ambele pare. avem
avem  par si demonstram ca aceasta implica
par si demonstram ca aceasta implica  par.
par.
Etapa verificarii: Calculam
Etapa demonstratiei: Presupunem ca
Verificam prin calcul direct [luand, de exemplu, membrul stang si inmultind parantezele] identitatea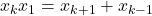 , iar din ea va rezulta
, iar din ea va rezulta 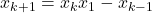 . Deoarece, conform presupunerii facute, membrul drept este par obtinem ca
. Deoarece, conform presupunerii facute, membrul drept este par obtinem ca  este si el par, ceea ce incheie demonstratia.
este si el par, ceea ce incheie demonstratia.
c) De este vorba?
este vorba?
c)Da este vorba despre a la puterea n
Multumesc pentru raspuns!