Rezolvati ecuatia: log3(5^x – 2) = log5(3^x + 2) unde x apartine lui R.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Foarte frumoasa rezolvare, domnule Blaugranas!
In privinta acelei functii, voi incerca sa demonstrez urmatorul rezultat. Poate va va ajuta candva. Fie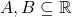 .Daca
.Daca 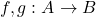 , cu
, cu 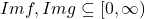 sunt strict crescatoare (descrescatoare) atunci
sunt strict crescatoare (descrescatoare) atunci 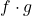 este strict crescatoare (descrescatoare).
este strict crescatoare (descrescatoare). 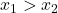 . Atunci avem
. Atunci avem 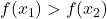 si
si 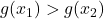 . Cum ambii membri ai fiecarei inegalitati sunt pozitivi, inmultim inegalitatile si obtinem
. Cum ambii membri ai fiecarei inegalitati sunt pozitivi, inmultim inegalitatile si obtinem 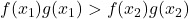 , adica si functia
, adica si functia 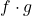 este strict crescatoare.
este strict crescatoare. .
.
Demonstratie: Fie
Pentru descrescatoare se procedeaza analog, luand, de exemplu,
Revenind la functia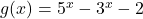 avem
avem ![Rendered by QuickLaTeX.com g(x)=3^x[(\frac{5}{3})^x-1]-2](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-4ebfd81c318debfbb620811255617935_l3.png) si cum functiile
si cum functiile 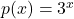 si
si 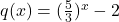 sunt strict crescatoare (
sunt strict crescatoare ( este exponentiala cu baza supraunitara, iar
este exponentiala cu baza supraunitara, iar  este suma (diferenta) dintre o functie exponentiala cu baza supraunitara si o functie constanta), rezulta, conform rezultatului demonstrat anterior, ca
este suma (diferenta) dintre o functie exponentiala cu baza supraunitara si o functie constanta), rezulta, conform rezultatului demonstrat anterior, ca 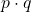 este si ea o functie strict crescatoare si urmeaza faptul ca
este si ea o functie strict crescatoare si urmeaza faptul ca  este si ea strict crescatoare fiind suma (diferenta) dintre o functie strict crescatoare si o functie constanta.
este si ea strict crescatoare fiind suma (diferenta) dintre o functie strict crescatoare si o functie constanta.
Frumos PhantomR … niciodata nu m-am gandit la chestii de genu` asta. (tot foloseam derivate).
Va multumesc! Sper sa fie si corect😀 . Banuiesc ca este mai usor cu derivate decat asa, dar probabil foloseste si asta la ceva pentru cei care nu cunosc analiza.