Salut!
Am 2 probleme legate de numere complexe si nu reusesc sa le gasesc o rezolvare.
Prima ar fi o ecuatie de gradul II:
![]() De aici nu stiu cum sa continui. Trebuie sa imi dea -1+i si 2i.
De aici nu stiu cum sa continui. Trebuie sa imi dea -1+i si 2i.
A 2-a problema este una de geometrie.
Enunt: Demonstrati ca oricare ar fi z apartine multimii numerelor complexe diferite de zero, imaginile geometrice ale numerelor complexe
![]()
Acum calculez distanta dintre fiecare 2 puncte consecutive inclusiv distanta dintre primul si ultimul punct. Aceasta distanta trebuie sa fie aceeasi pentru ca punctele sa fie varfurile unui romb.
![]() Problema e ca AB nu este egal cu BC asa cum ar fi trebuit. Nu sunt sigur de acea formula. Adica nu stiu daca se aplica si la numere complexe.
Problema e ca AB nu este egal cu BC asa cum ar fi trebuit. Nu sunt sigur de acea formula. Adica nu stiu daca se aplica si la numere complexe.
Multumesc.
P.S. Problemele sunt luate dintr-o carte pentru bac Matematica pentru examenul de bacalaureat ; editura :clubul matematicienilor; autori: Marian Andronache, Dinu Serbanescu, Marius Perianu, Catalin Ciupala, Florian Dumitrel. Pagina 32 respectiv 33, exercitiile 9 h) respectiv 16.


Solutiile unei ecuatii de gradul doi de forma cu
cu 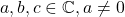 sunt date de:
sunt date de: 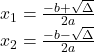 .
.
In cazul problemei de fata avem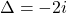 . Trebuie sa gasim numarul complex
. Trebuie sa gasim numarul complex 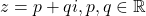 astfel incat
astfel incat 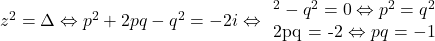 . Trecand la module din prima relatie obtinem
. Trecand la module din prima relatie obtinem 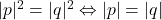 si trecand la module si in a doua obtinem
si trecand la module si in a doua obtinem 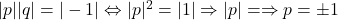 . Pentru
. Pentru 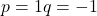 . Pentru
. Pentru 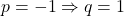 . Asadar avem
. Asadar avem 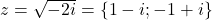 . Deci radacinile ecuatiei sunt
. Deci radacinile ecuatiei sunt 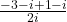 si
si 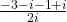 , adica
, adica 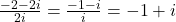 si
si 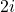 .
.
Multumesc mult PhantomR!
Cu cea mai mare placere!:) Sper sa se inteleaga ceva.. eu stau rau cu explicatiile. O metoda mai „simpluta” de a rezolva acel radical era sa observati direct ca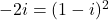 .
.
La 2 lipseste ceva din cerinta cred🙂 .
Da, asa e. Probleme ale sistemului meu (ale PC-ului). Cerinta era ca acele puncte sa fie varfurile unui romb. Problema e ca nu se verifica. AB si BC nu sunt egale, dupa cum vezi. Dar nu sunt sigur de acea formula. Adica nu sunt sigur ca se poate utiliza formula aceea la numere complexe.
P.S. Ai fost anul trecut la olimpiada nationala (de matematica) de la Oradea?
Iti las un mesaj privat🙂 .
Ai vreo idee de rezolvare la 2? I mean…poate este vreo formula de calculare a distantei….vreo formula legata de module?🙄
Cosmin. Ordinea pe care ai ales-o nu e buna. Tb sa iei pct astfel.
(0,0) (a,-b) (2a,0) (a,b) sau invers : (0,0) (a,b) (2a,0) (a,-b)
Da, am inteles. Eu am luat ordinea in care sunt date punctele in problema. Nu m-am gandit sa schimb ordinea. Multumesc!
Imi cer iertare ca nu am raspuns si in legatura cu problema doi in celalalt post. Cred ca domnul Blaugranas are dreptate.
Eu cred ca merge acea formula. O alta idee:
Folosind notatiile tale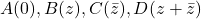 avem
avem 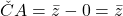 si
si 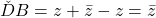 . Deci avem
. Deci avem 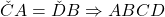 paralelogram (dar cu notatiile cam „ciudate”, adica in plan va aparea probabil ceva de genul
paralelogram (dar cu notatiile cam „ciudate”, adica in plan va aparea probabil ceva de genul 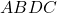 , in aceasta ordine). Cum paralelogramul cu doua laturi consecutive congruente este romb mai ramane de aratat, de exemplu, ca
, in aceasta ordine). Cum paralelogramul cu doua laturi consecutive congruente este romb mai ramane de aratat, de exemplu, ca 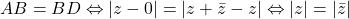 , adevarat. In concluzie patrulaterul este intr-adevar romb.
, adevarat. In concluzie patrulaterul este intr-adevar romb.
Nu e bine PhantomR. AC=BD sunt diagonale. => Tb sa arati ca AB=AD si nu prea sunt egale. Scuze mi s-a parut. E bine si asha.
Nu e nicio problema. Intr-adevar e cam ciudata (neobisnuita mai bine zis probabil) ordinea.
Nu e ciudat e un puzzle. Ce farmec avea prb daca toate pct erau date in ordinea corecta??? era pur si simplu de facut o verificare.
Dap, asa e. Fara dexteritate sau mai bine zis perspicacitate nu cred ca se putea rezolva problema asta. Anyway, multumesc mult amandurora pentru efort!
@Blaugranas: Da, cred ca aveti dreptate🙂 .
@Cosmin_NTG: Frumos punct de vedere! Cu cea mai mare placere! Oricand!